| << Chapter < Page | Chapter >> Page > |
| 1 | 0 | |||||
| 0 | 1 | 0 | ||||
| 0 | 1 | 0 |
These values are useful when asked to solve a problem involving trig functions without using a calculator.
Each of the trigonometric functions has a reciprocal that has a special name. The three reciprocals are cosecant (or cosec), secant (or sec) and cotangent (or cot). These reciprocals are given below:
We can also define these reciprocals for any right angled triangle:
Find the length of x in the following triangle.

In this case you have an angle ( ), the opposite side and the hypotenuse.
So you should use
Use the sin button on your calculator
Find the value of in the following triangle.

In this case you have the opposite side and the hypotenuse to the angle .
So you should use
Since you are finding the angle ,
use on your calculator
Don't forget to set your calculator to `deg' mode!
In the previous example we used . This is simply the inverse of the tan function. Sin and cos also have inverses. All this means is that we want to find the angle that makes the expression true and so we must move the tan (or sin or cos) to the other side of the equals sign and leave the angle where it is. Sometimes the reciprocal trigonometric functions are also referred to as the 'inverse trigonometric functions'. You should note, however that and are definitely NOT the same thing.
The following videos provide a summary of what you have learnt so far.
Trigonometry - 1
Khan academy video on trigonometry - 2
Find the length of the sides marked with letters. Give answers correct to 2 decimal places.


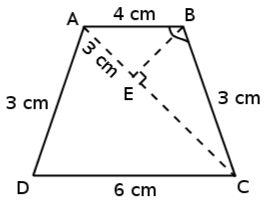
We can use the trig functions to solve problems in two dimensions that involve right angled triangles. For example if you are given a quadrilateral and asked to find the one of the angles, you can construct a right angled triangle and use the trig functions to solve for the angle. This will become clearer after working through the following example.
Let ABCD be a trapezium with , , and . Point E on diagonal AC divides the diagonal such that . Find .

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?