| << Chapter < Page | Chapter >> Page > |
We illustrate the dynamics of the synaptic conductance in a very simple example presented in Figure 1.

Similar to the network current, the external current for cell is given by
where
We assume that all external sources are excitatory and have the same reversal potential, . This assumption allows us to model the sum of the effects of all external sources as a single effective excitatory synapse with peak conductance and decay constant . The external firing rate, , now represents the sum of the firing rates of all external sources. Because the external sources have no input in this model, we must generate their spike trains. To meet this end, we set to be a Poisson spike train with mean rate .
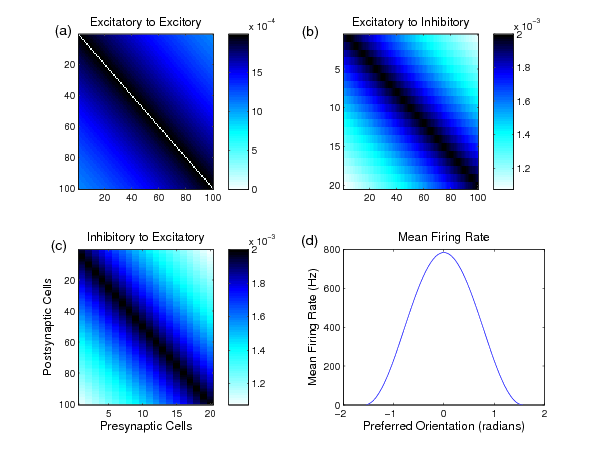
We now apply this network model to a network of cells found in a hypercolumn in primary visual cortex. We divide the network neurons into two types: excitatory and inhibitory. Each cell is selective to the orientation of the visual stimulus and is parameterized by its preferred orientation (PO). For excitatory neurons, the PO for cell is given by , and the reversal potential is uniform and denoted . The PO and reversal potential for inhibitory neurons are defined analogously.
The peak conductance at a network synapse is dependent on the PO of the pre- and postsynaptic neurons. If cell is excitatory, then the peak conductance at the excitatory synapse from cell to cell is given by
where is the excitatory decay constant in space. The peak conductance at inhibitory synapses is defined analogously. We assume that no cell synapses onto itself, or , and that no inhibitory to inhibitory synapses exist. Figure 2 shows the network architecture for a small network.
Excitatory neurons in the lateral geniculate nucleus (LGN) are the external sources for our network in the primary visual cortex. The total mean firing rate of all external sources to cell is given by
where is the PO of cell , and is the orientation of the stimulus. The parameter dictates the stimulus contrast, and the parameter measures the degree of tuning of the LGN input. The maximum firing rate, , is reached if and . Note that if , the LGN input is untuned, and if , the LGN input vanishes when .
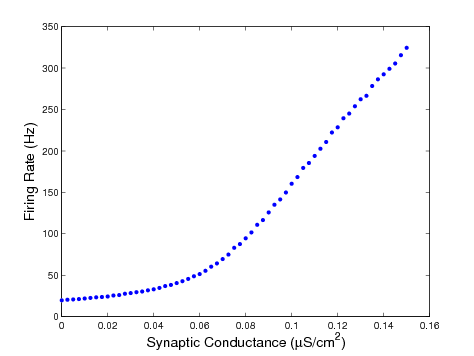
To ensure that we have understood and implemented the model as Shriki intended, we now test our model by reproducing the conductance-based portion of Figure 3 in Shriki's paper [link] . For this simple example, the network in the primary visual cortex consists of excitatory, homogeneous neurons. The homogeneity of the network means that each neuron is connected to every other neuron with peak conductance . Also, each neuron has the same PO, implying that the mean firing rate, , is uniform across all neurons. To model this, we generate uncorrelated Poisson spike trains with mean firing rate . We now implement the model for this homogeneous network to show how the firing rate depends on the peak synaptic conductance, Our results are shown in Figure 3.
| 1000 | |
| 0.0035 | |
| 1570 Hz | |
| 5 rad | |
| 5 ms | |
| 5 ms | |
| -73 mV | |
| 1 | |
| -65 mV |
We have shown how to extend the model of the isolated single compartmental neuron to model a network of neurons receiving external input. Using this model, we have simulated the dynamics of a network of cells in the primary visual cortex receiving input from the LGN. For an excitatory, homogeneous network, we have shown the relationship between the firing rate of the network and the peak synaptic conductance at the network synapses, reproducing results obtained by Shriki et al. The next step needing to be taken for this VIGRE project is to implement the rate equations that are the central focus of the Shriki paper. We could then compare the results obtained from the rate model to those obtained in the conductance-based model presented here and determine if the rate equations are a good approximation for the conductance-based model.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?