This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses division of fractions. By the end of the module students should be able to determine the reciprocal of a number and divide one fraction by another.
Section overview
- Reciprocals
- Dividing Fractions
Reciprocals
Reciprocals
Two numbers whose product is 1 are called
reciprocals of each other.
Sample set a
The following pairs of numbers are reciprocals.
Notice that we can find the reciprocal of a nonzero number in fractional form by inverting it (exchanging positions of the numerator and denominator).
Practice set a
Find the reciprocal of each number.
Dividing fractions
Our concept of division is that it indicates
how many times one quantity is contained in another quantity. For example, using the diagram we can see that there are 6 one-thirds in 2.
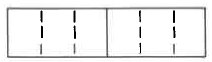 There are 6 one-thirds in 2.
There are 6 one-thirds in 2.
Since 2 contains six
's we express this as
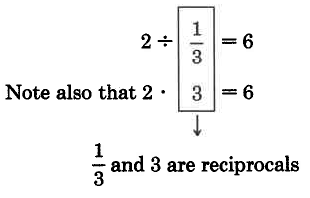
Using these observations, we can suggest the following method for dividing a number by a fraction.
Dividing one fraction by another fraction
To divide a first fraction by a second, nonzero fraction, multiply the first traction by the reciprocal of the second fraction.
Invert and multiply
This method is commonly referred to as
"invert the divisor and
multiply."
Sample set b
Perform the following divisions.
. The divisor is
. Its reciprocal is
. Multiply
by
.
Got questions? Get instant answers now!
The divisor is
. Its reciprocal is
. Multiply
by
.
Got questions? Get instant answers now!
. The divisor is
. Its reciprocal is
. Multiply
by
.
Got questions? Get instant answers now!
. Convert each mixed number to an improper fraction.
.
.
The divisor is
. Its reciprocal is
. Multiply
by
.
Got questions? Get instant answers now!
. First conveniently write 8 as
.
The divisor is
. Its reciprocal is
. Multiply
by
.
Got questions? Get instant answers now!
. The divisor is
. Its reciprocal is
.
Got questions? Get instant answers now!
How many
-inch-wide packages can be placed in a box 19 inches wide?
The problem is to determine how many two and three eighths are contained in 19, that is, what is
?
Convert the divisor
to an improper fraction.
Write the dividend 19 as
.
The divisor is
. Its reciprocal is
.
Thus, 8 packages will fit into the box.
Got questions? Get instant answers now!
Practice set b
Perform the following divisions.
A container will hold 106 ounces of grape juice. How many
-ounce glasses of grape juice can be served from this container?
Got questions? Get instant answers now!
Determine each of the following quotients and then write a rule for this type of division.
Exercises
For the following problems, find the reciprocal of each number.
For the following problems, find each value.
or
Got questions? Get instant answers now!
or
Got questions? Get instant answers now!
or
Got questions? Get instant answers now!
Exercises for review
![]() There are 6 one-thirds in 2.
There are 6 one-thirds in 2.
