0.1 Kirchhoff's circuit laws (Page 3/3)

Electricity and magnetism Page 3 / 3

We conclude that if DOT and DOC are same then potential difference across resistor is negative and if they are opposite then the potential difference across resistor is positive.

The sign of power source is easier to decide. It merely depends on the direction of travel (DOT). Moving across a EMF source from negative to positive terminal is like moving from a point of lower to point of higher potential. Thus, if traveling across a source, we move from negative to positive terminal then potential difference is positive otherwise negative.

Combining above considerations, we write KVL equations for loops ABCFA and EDCFE as :

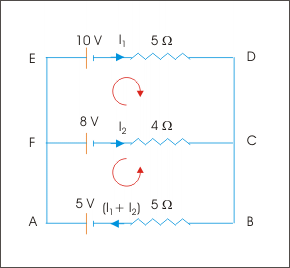
Loop EDCFE (Starting from E) :

$\sum V = - 10 - 5 I_{1} + 4 I_{2} + 8 = 0$ $5 I_{1} - 4 I_{2} = - 2$

Loop ABCFA (Starting from A) :

$\sum V = - 5 + 5 (I_{1} + I_{2}) + 4 I_{2} + 8 = 0$ $\Rightarrow 5 (I_{1} + I_{2}) + 4 I_{2} = - 3$ $\Rightarrow 5 I_{1} + 9 I_{2} = - 3$

Subtracting first from second we eliminate $I_{1}$ and we have :

$\Rightarrow 13 I_{2} = - 1$ $\Rightarrow I_{2} = - \frac{1}{13} A$

Current in ED,

$\Rightarrow I_{1} = \frac{(- 2 + 4 I_{2})}{5} = \frac{(- 2 + 4 X \frac{- 1}{13})}{5} = - \frac{6}{13} A$

Current in BA,

$\Rightarrow (I_{1} + I_{2}) = - \frac{1}{13} - \frac{6}{13} = - \frac{7}{13} A$

Clearly, direction of current in each of the branch are opposite to the ones assumed.

Problem : Consider the network of resistors as shown here :

Network of resistors connected to EMF source

Each resistor in the network has resistance 2 Ω. The EMF of battery is 10 V having internal resistance 1/6 Ω. Determine the equivalent resistance of the network.

Solution : We have seen in the earlier example that if I be the current, then current is distributed in different branches of the network as shown in the figure.

Clearly, we need to determine current I in order to calculate equivalent resistance of the network. For this, we consider the loop ABCMA in clockwise direction. Applying KVL :

$\sum V = - \frac{I}{3} - \frac{I}{6} - \frac{I}{3} - I X \frac{1}{6} + 10 = 0$ $\Rightarrow \frac{5 I}{6} + \frac{I}{6} = 10$ $\Rightarrow I = 10 A$

Let $R_{e q}$ be the equivalent resistance of the network. Reducing given circuit and applying KVL in clockwise direction, we have :

$\sum V = - 10 X R_{e q} - 10 X \frac{1}{6} + 10 = 0$ $\Rightarrow R_{e q} = \frac{50}{60} = \frac{5}{6} Ω$

Exercise

Consider the network of resistors as shown here :

Determine the equivalent resistance of the network between A and C.

In order to determine equivalent resistance, we assume that given network is connected to an external source of EMF equal to E. Now, the external EMF is related to effective resistance as :

$E = I R_{e q}$

Once this relation is known, we can determine equivalent resistance of the given network. It is important to note that current distribution is already given in the problem figure.

Considering loop ABCEA in clockwise travel, we have KVL equation as :

$\sum V = - I_{1} R_{1} - I_{2} R_{2} + E = 0$ $\Rightarrow E = I_{1} R_{1} + I_{2} R_{2}$

Considering loop ABDA in clockwise travel, we have KVL equation as :

$\sum V = - I_{1} R_{1} - (I_{1} - I_{2}) R_{3} + I_{2} R_{2} = 0$

We solve for $I_{2}$ to get an expression for it in terms of $I_{1}$ as :

$\Rightarrow I_{2} = \frac{I_{1} (R_{1} + R_{3})}{(R_{2} + R_{3})}$

Substituting above expression of $I_{2}$ in the equation obtained earlier for E, we have :

$\Rightarrow E = I_{1} R_{1} + \frac{I_{1} (R_{1} + R_{3}) R_{2}}{(R_{2} + R_{3})}$ $\Rightarrow I_{1} = \frac{(R_{2} + R_{3}) E}{[R_{3} (R_{1} + R_{2}) + 2 R_{1} R_{2}]}$

Putting this expression for $I_{1}$ in the expression obtained earlier for $I_{2}$ , we have :

$\Rightarrow I_{2} = \frac{(R_{1} + R_{3}) E}{[R_{3} (R_{1} + R_{2}) + 2 R_{1} R_{2}]}$

But, we know that :

$I = I_{1} + I_{2}$

$\Rightarrow I = \frac{(R_{1} + R_{2} + 2 R_{3}) E}{[R_{3} (R_{1} + R_{2}) + 2 R_{1} R_{2}]}$

Thus,

$\Rightarrow R_{e q} = \frac{E}{I} = \frac{[R_{3} (R_{1} + R_{2}) + 2 R_{1} R_{2}]}{(R_{1} + R_{2} + 2 R_{3})}$

Consider the network of resistors and batteries as shown here :

Find the currents in different braches of the network.

We assign currents with directions in different branches as shown in the figure. We can, however, assign current directions in any other manner we wish. Here, starting from $I_{1}$ and $I_{2}$ in branches CA and AB respectively and applying KCL at A, the current in AD is $I_{1} - I_{2}$ . Let the current in FE is $I_{3}$ . Applying KCL at B, current in BC is $I_{2} + I_{3}$ . Again applying KCL at C, current in CD is $I_{2} + I_{3} - I_{1}$ .

Considering loop ABCA in clockwise travel, we have KVL equation as :

$\sum V = - 2 I_{2} - 1 (I_{2} + I_{3}) - 2 I_{1} + 20 = 0$ $\Rightarrow 2 I_{1} + 3 I_{2} + I_{3} = 20$

Considering loop ADCA in anticlockwise travel, we have KVL equation as :

$\sum V = - 2 (I_{1} - I_{2}) + (I_{2} + I_{3} - I_{1}) - 2 I_{1} + 20 = 0$ $\Rightarrow 5 I_{1} - 3 I_{2} - I_{3} = 20$

Considering loop BCDFEB in anticlockwise travel, we have KVL equation as :

$\sum V = - (I_{2} + I_{3}) - (I_{2} + I_{3} - I_{1}) + 10 - 2 I_{3} = 0$ $\Rightarrow - I_{1} + 2 I_{2} + 4 I_{3} = 10$

We have three equations with three variables. Solving, we have :

$I_{1} = 40 / 7 A; I_{2} = 13 / 7 A; I_{3} = 3 A$

Currents in different branches are :

$I_{C A} = I_{1} = \frac{40}{7} A; I_{A B} = I_{2} = \frac{13}{7} A$ $I_{A D} = I_{1} - I_{2} = \frac{40}{7} - \frac{13}{7} = \frac{27}{7} A$ $I_{B C} = I_{2} + I_{3} = \frac{13}{7} + 3 = \frac{34}{7} A$ $I_{C D} = I_{2} + I_{3} - I_{1} = \frac{34}{7} - \frac{40}{7} = - \frac{6}{7} A$ $I_{D F E B} = I_{3} = 3 A$

Note that current in branch CD is negative. It means that current in the branch is opposite to the assumed direction.

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Electricity and magnetism. OpenStax CNX. Oct 20, 2009 Download for free at http://cnx.org/content/col10909/1.13

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Electricity and magnetism' conversation and receive update notifications?

Ask

	20 Sociology 20 Population Urbanization Environment By OpenStax Start Quiz
	4 Sociology 04 Society and Social Interaction MCQ By OpenStax Start Quiz
	Pre-class Online Quiz - Case Control Studies By Mucho Mizinduko Start Quiz
	Excel 2007 Quiz By Lakeima Roberts Start Quiz
	1 Neuroscience Exam 2004 1 By David Corey Start Exam
	5 Microbiology Final Practice By Madison Christian Start Assignment
	9 BOD- Liver Quiz .... By Brooke Delaney Start Quiz
©flickr:	Microbiology Final By Szilárd Jankó Start Quiz
©flickr:	Vocabulary Practice Quiz! By Katie Montrose Start Quiz
	5 Lec:5 Case-control Studies By Janet Forrester Start Quiz

0.1 Kirchhoff's circuit laws (Page 3/3)

Voltage across circuit elements

Network of resistors

Network of resistors

Equivalent resistance

Exercise

Electrical network

Electrical network

Electrical network

Electrical network

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!