| << Chapter < Page | Chapter >> Page > |
3.2
250 mm
320 mm
3.3
a) 135 mm
b) 135 mm
c) 104 mm
d) 174 mm
3.4
a) area = 2 x (b + d) or area = (2 x b) + (2 x d)
b) area= 2 x (f+g) or area = (2 x f) + (2 x g)
c) area = 4 x k
d) area = (2 x a) + (2 x e) or area = 2 x (a + e)
3.5
By means of a piece of string or wool
3.6
a) 3 100 km
b) 500 km
c) 350 km
d) 15,45 h
38.
a) 42
b) own answer
c) R2,681,70
5.
a) 27
b) 27
c) 39
d) 18
e) 18
f) 9
g) 14
h) 2
i) 12
j) 60
k) 60
l) 64
m) 72
n) 125
o) 108
3. PERIMETER
3.1 IMPORTANT to REMEMBER!
The perimeter of any figure is the total length around a figure, in other words the sum of the lengths of all the sides.
Perimeter is thus a length and is measured in millimetres, metres or kilometres. The most accurate method to determine perimeter is to use compasses and a ruler.

3.2 What is the perimeter of your pentagon and octagon above?
Pentagon:
Octagon:
3.3 Use your ruler and determine the perimeter of the following polygons:
a)
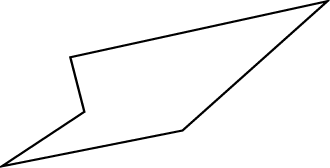
______________________________________

_____________________________________
c)

_____________________________________

_____________________________________
3.4 Work together with a friend. Work out formulas to determine the perimeters of the following quadrilaterals:
a) A rectangle with a length of b centimetres and breadth of d centimetres:
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
b) A parallelogram with sides f centimetres and g centimetres:
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
c) A rhombus with sides k millimetres:
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
d) A kite with sides a millimetres and e millimetres:
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
3.5 How will you determine the perimeter of the following figures?
a)

b)

______________________________________________________________
______________________________________________________________
______________________________________________________________
3.6 A grade 7 class leaves on a tour.
a) Look at the accompanying sketch and use the scale to find out how far they will travel.

1 : 100
1 cm = 100km
b) What is the actual distance from E to B? _____________________________
c) What is the actual distance from B to D? _____________________________
c) If the bus travels at 110 km/h, how long will it take for the bus to travel from A to F if it doesn’t stop along the way?
____________________________________________________________________
3.8 The sketch shows a camp for sheep that needs to be fenced.

a) If the horizontal poles are 2,7 m long, and you leave an opening of 1,5 m for a gate, how many upright poles are you going to need?
_____________________________________________________________________
_____________________________________________________________________
b) Where are you going to leave an opening for a gate? Motivate your answer.
_____________________________________________________________________
_____________________________________________________________________
c) If the upright poles cost R63,85 each, how much will the farmer have to spend?
_____________________________________________________________________
_____________________________________________________________________
4. Time for self-assessment
|
Yes | No |
| I could find solutions to the brainteasers. | ||
| I was able to draw a regular pentagon. | ||
| I was able to draw a regular octagon. | ||
| I can explain the concept “perimeter”. | ||
| I could calculate accurately the perimeter of the polygons. | ||
| I was able to formulate and write down the formulas for perimeter of the following: | ||
|
||
|
||
|
||
|
||
| I was able to calculate accurately, according to scale, the distance that the Grade 7’s would have covered on their tour. | ||
| I was able to correctly calculate the number of poles that the farmer needed for his camp. |
5. Let us test your mental maths now!
Complete the following as quickly and accurately as possible:
a) 6 + 7 x 3 = ............
b) 6 + (7 x 3) = ............
c) (6 + 7) x 3 = ............
d) 9 x 6 ÷ 3 = ............
e) 9 x (6 ÷ 3) = ............
f) 36 ÷ (12 ÷ 3) = ............
g) 13 – 5 + 6 = ............
h) 13 – (5 + 6) = ............
i) 14 – (5 – 3) = ............
j) 4 x 3 x 5 = ............
k) 5 x (3 x 4) = ............
l) 43 = ............
m) 32 x 23 = ............
n) 53 = ............
o) 33 x 22 = ............
| I did | WELL | REASONABLY | NOT SO WELL |
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.5: We know this when the learner solves or completes number sentences by inspection or by trial-and-improvement, checking the solutions by substitution (e.g. 2 x - 8 = 4).
Learning Outcome 4: The learner will be able to use appropriate measuring units, instruments and formulae in a variety of contexts.
Assessment Standard 4.2: We know this when the learner solves problems;
Assessment Standard 4.3: We know this when the learner solves problems using a range of strategies;
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.8: We know this when the learner performs mental calculations involving squares of natural numbers to at least 10 2 and cubes of natural numbers to at least 5 3 .

Notification Switch
Would you like to follow the 'Mathematics grade 7' conversation and receive update notifications?