| << Chapter < Page | Chapter >> Page > |
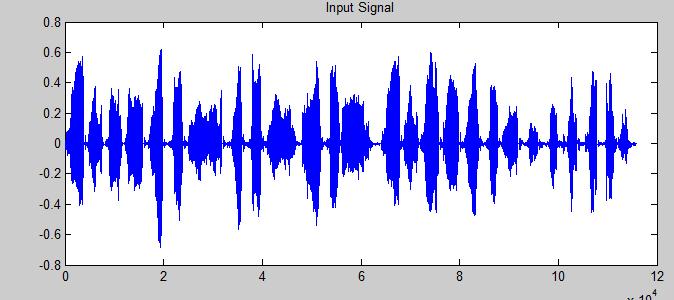
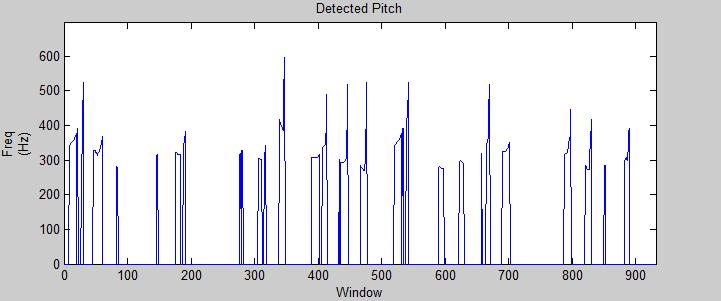
The PSOLA pitch correction algorithm requires both an original pitch and a "target" pitch to achieve. If this were a fully-automated pitch-smoothing autotuner, the target pitch would be whatever "note" frequency was closest to the one observed. We on the other hand would like to bend the pitch to the specific frequency of the song, regardless of our starting point. To this end, we must generate a vector of desired frequencies.
Fortunately, thanks to our song interpretation earlier, we already have vectors of the pitch and length of each note in the song at hand. These vectors assume the following format:
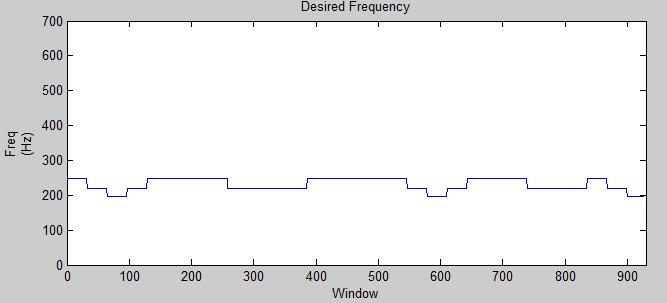
First, we generate a vector of frequencies for each sample at our defined sampling rate. This is as simple as producing a vector with a length equal to the total length of the song in seconds times the sampling frequency (thus, lengthN = sum(durations)*Fs). Then, for each note, we copy the frequency of that note over every sample in the vector for a range of the note's duration. This is most easily done using MatLab's "cumsum" function on the durations vector to make each note indexed by the cumulative time passed, and then multiply these by the sampling frequency to produce the index of each note in samples.
Now that we have the frequency for every sample, we can chop up this full-length signal into windows just as we did to the input signal. For each window's range, we simply take the mode of the frequencies in that range (given their short length, a window will never span more than two notes) and let that be the desired frequency for that window.
Now that we have our original and target frequencies, we can exercise the Pitch-Synchronous Overlap Add algorithm to attempt to correct the frequencies. Like autocorrelation, the PSOLA begins with a windowed, segmented signal. Because we have already determined pitches for a specific number of segments, the PSOLA computations will use the same segment length. This is easy to remember, but introduces some issues. For example, the PSOLA algorithm can make the finest pitch corrections with a greater number of smaller segments, allowing for smoother correction across the signal. But what would happen to the autocorrelation pitch detector if the segment was so small that a full period could not be obtained? A compromise must be made on a segment length which allows for optimal pitch detection and pitch correction, with guesswork as the only means of finding the "happy medium".
The PSOLA algorithm described here is the Time-Domain PSOLA. Alternative PSOLA methods exist which depend on linear predictor coefficients rather than segmented waves. The TD-PSOLA is used for its simplicity in programming versus marginal increase in computational cost.
Gareth Middleton, "Pitch Detection Algorithms," Connexions, December 17, 2003, (External Link)
Lemmetty, Sami. Review of Speech Synthesis Technology. (Master’s Thesis: Helsinki University of Technology) March 1999. (External Link)
Upperman, Gina. "Changing Pitch with PSOLA for Voice Conversion." Connexions. December 17, 2004. (External Link)

Notification Switch
Would you like to follow the 'Speak and sing' conversation and receive update notifications?