| << Chapter < Page | Chapter >> Page > |

Looking for a thrill? Then consider a ride on the Singapore Flyer, the world’s tallest Ferris wheel. Located in Singapore, the Ferris wheel soars to a height of 541 feet—a little more than a tenth of a mile! Described as an observation wheel, riders enjoy spectacular views as they travel from the ground to the peak and down again in a repeating pattern. In this section, we will examine this type of revolving motion around a circle. To do so, we need to define the type of circle first, and then place that circle on a coordinate system. Then we can discuss circular motion in terms of the coordinate pairs.
To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in [link] . The angle (in radians) that intercepts forms an arc of length Using the formula and knowing that we see that for a unit circle ,
Recall that the x- and y- axes divide the coordinate plane into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.
For any angle we can label the intersection of the terminal side and the unit circle as by its coordinates, The coordinates and will be the outputs of the trigonometric functions and respectively. This means and
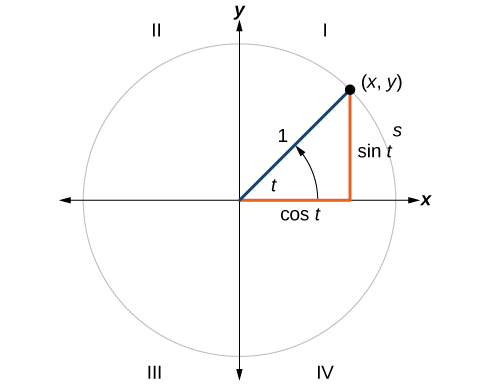
A unit circle has a center at and radius . In a unit circle, the length of the intercepted arc is equal to the radian measure of the central angle
Let be the endpoint on the unit circle of an arc of arc length The coordinates of this point can be described as functions of the angle.
Now that we have our unit circle labeled, we can learn how the coordinates relate to the arc length and angle . The sine function relates a real number to the y -coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle equals the y -value of the endpoint on the unit circle of an arc of length In [link] , the sine is equal to Like all functions, the sine function has an input and an output. Its input is the measure of the angle; its output is the y -coordinate of the corresponding point on the unit circle.
The cosine function of an angle equals the x -value of the endpoint on the unit circle of an arc of length In [link] , the cosine is equal to
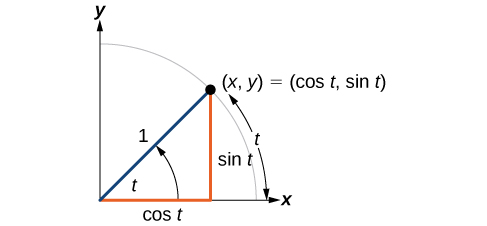
Because it is understood that sine and cosine are functions, we do not always need to write them with parentheses: is the same as and is the same as Likewise, is a commonly used shorthand notation for Be aware that many calculators and computers do not recognize the shorthand notation. When in doubt, use the extra parentheses when entering calculations into a calculator or computer.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?