| << Chapter < Page | Chapter >> Page > |
The easiest case consists in reducing the sampling rate by simply dropping samples.This procedure is called Downsampling . However, we need to be careful on the effect of this procedure. We note immediately,that the new sampling rate needs to be still above Nyquist, i.e., in order to avoid aliasing.
Effect in the frequency domain In continuous time, downsampling the signal corresponds to passing to the signal . Indeed, sampling at the same frequency as we obtain the samples as we should. In summary, using the properties of the Fourier transform
This tells us, that the spectral copies of (the Fourier transform of the sampled signal ) should have the same overall shapeand at the same distance as those of , but they are stretched in frequency by a factor and squeezed in amplitude by a factor .
Indeed, we arrive at the same conclusion computing via the sampled signals, using [link] :
Recall that , the Fourier transform of sampled at frequency , looks like except that its spectral copies lie at distance , thus times closer than those of .
For the discrete Fourier Transform we should expect to see roughly the same behavior. Recall, though, that the relation between continuous and discrete Fourier transform is only approximative.
Aliasing : We give two examples.
First, downsampling to a sampling rate that is too low can lead to aliasing. Downsampling the image of [link] left leads to the same effect as visible in the same figure center.
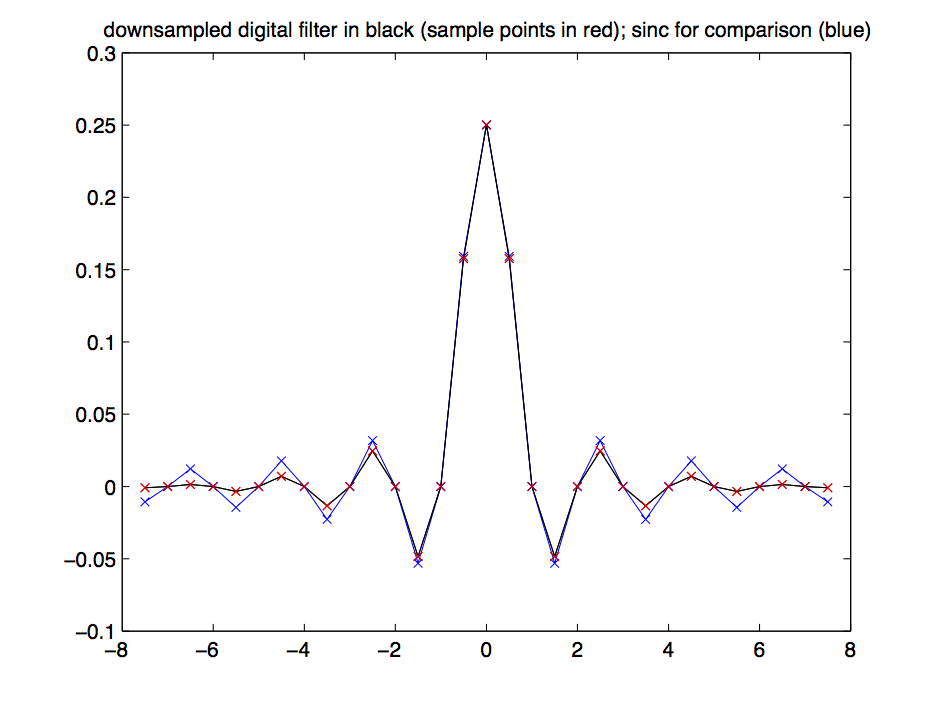
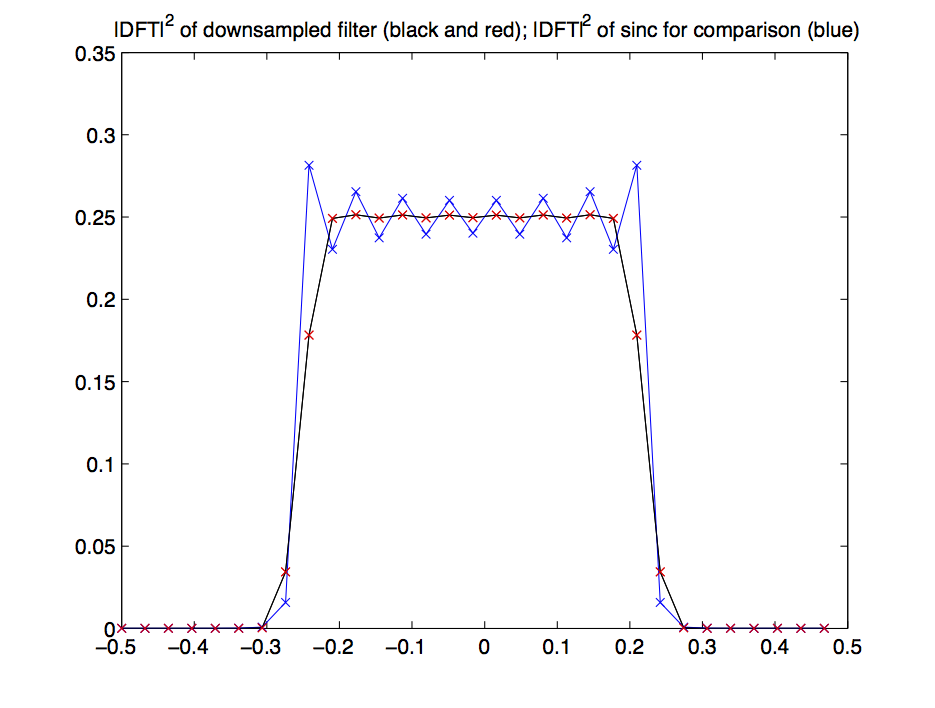
Second, downsampling a simple signal such as the filter of [link] by results in a new filter with twice the cutoff frequency, i.e. , but with a value over the pass-band, thus a power spectral value over the pass-band (see [link] ). No aliasing occurs since the condition is satisfied.
Power : We consider first the case of a -periodic signal . Then, has period . Substituting with we get
From the simple properties we know
(same complex amplitudes
There is no contradiction between
and
. Both express that
, both allow to
conclude that power does not change under downsampling, and both imply thatthe DFT of
is
times smaller and corresponds to frequencies which
are
times further apart than those of
. Indeed, using
[link] we get
Note that the energy of a finite energy signal would change under downsampling: computing in time
A simliar computation can be done in frequency. See Comment 6 .
Comment 6 Computing in frequency with and :
For a discrete signal we are naturally in the periodic case. From the above we should expect that power stays approximatively the same under downsampling provided that . Also, we noted earlier that power should not dependon the sampling rate, as long as the samples faithfully represent the signal, and at least approximatively.
For the simple signal , the filter from [link] , we may verify this explicitly. Denote the downsampled filter by (see [link] for an illustration with ). Since no aliasing occurs during downsampling, the pass-band is now times longer, meaning that times more of the are different from zero (this makes the power increase by ). Further, their power spectral values are by smaller (this makes the power decrease by ). Finally, the sample length is now times shorter (this increases the power my ; recall [link] ).
All in all, power is not changed, at least approximatively.One finds which has to be compared to the power of the original filter.
To obtain a low-pass filter one would have to normalize to .
Let us now drop the assumption .
To resample a signal at an times lower rate, a first attempt would be to discard all but every -th sample: . This step is called downsampling as we have seen above. However, to avoid aliasing effects caused by downsampling below Nyquist ratea low-pass filtering at cutoff is required before downsamling. The filter used is called anti-aliasing filter . The new utilized bandwidth will be only .
The procedure of first applying an anti-aliasing filter and then downsampling is called decimation .
Agreeably, the filtering before downsampling destroys information about . However, this loss occurs in a controllable manner: It removes high-frequencyinformation. For an audio signal, we loose the high pitch sound. For an image we loose sharpness of edges. This should be compared to an uncontrolled lossof quality when no anti-aliasing filter is applied (see [link] ).
In summary, Decimation by means to resample at times lower rate and consists of two steps:
Low-pass filtering will reduce power, as high frequencies are attenuated. Down-sampling will leave the new power roughly the same.
The matlab commands are
decimate and
downsample .

Notification Switch
Would you like to follow the 'Sampling rate conversion' conversation and receive update notifications?