| << Chapter < Page | Chapter >> Page > |
In order to investigate continuity at singularity point, we consider a function definition which is obtained by modifying modulus function :
| x; x>0
f(x) = || -x: x<0
Graph of function
The function is not defined for x=0. Singularity is a point where function is not defined. Thus, this point is singularity for the function which is otherwise defined for all other points on R. They are equal and are equal to a value which is not defined! In accordance with the definition, the limit of function exists at x=0 and is equal to zero. At this point, both left and right limits exist. After all, limit points to a value. Here, it points to a value outside the domain of function. See graph. Existence of limit at x=0, however, has nothing to do with continuity of function at that point as function is not defined at x=0 in the first place. This point is not the part of function definition i.e. its domain and hence continuity or discontinuity is not a concern.
We consider another function. This is modulus of reciprocal condition, f(x) = |1/x|. Using transformation technique, we draw of graph of function as shown :
Graph of function

The left and right limits both are positive infinity (read tending to infinity) at x=0. The limit of the function is infinity at this point. But, again point x=0 is not part of function definition. Hence, we say that function is continuous in its domain R-{0}.
Clearly, we need to distinguish between “discontinuous” and “undefined”. Going by two illustrations above, we need to understand that tangent, cotangent, secant and cosecant functions are continuous functions though they appear to be discontinuous graphically. They are not defined at certain values, but then these points are not the part of domain as well. As a matter of fact, rational functions, known to have singularities corresponding to points where denominator is zero, are continuous functions in their domain. For this reason, function such as reciprocal function "1/x" is a continuous function in its domain, which is R – {0}.
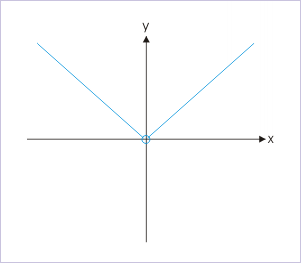
Continuity at a point does not guarantee that function is differentiable at the point. In order to understand this, we now consider the modulus function itself. Is function continuous at x=0? Is function is differentiable at x=0?
Graph of function

The limit of function is 0, which is finite and is equal to function value. Clearly, function is continuous at this point – thought we can not draw a tangent at this point and as such function is not differentiable at the point. The converse of the assertion, however, is true. If a function is differentiable at a point, then function is continuous at that point. Clearly, differentiability has stricter requirements than that of continuity.
A function is discontinuous if it is not continuous. We can fail the conditions of continuity in many ways. Accordingly, there are following types of discontinuity :

Notification Switch
Would you like to follow the 'Functions' conversation and receive update notifications?