| << Chapter < Page | Chapter >> Page > |
The learners must be able to:
1. identify and solve problems and make decisions using critical and creative thinking;
2. work effectively with others as members of a team, group, organisation and community;
3. organise and manage themselves and their activities responsibly and effectively;
4. collect, analyse, organise and critically evaluate information;
5. communicate effectively using visual, symbolic and/or language skills in various modes;
6. use science and technology effectively and critically, showing responsibility towards the environment and the health of others;
6. demonstrate an understanding of the world as a set of related systems by recognising that problem-solving contexts do not exist in isolation;
7. reflect on and explore a variety of strategies to learn more effectively;
8. participate as responsible citizens in the life of local, national, and global communities;
9. be culturally and aesthetically sensitive across a range of social contexts;
10. explore education and career opportunities; and
develop entrepreneurial opportunities.

You need: a wooden block, a large stone, a shoe, a book and a lunch box.
Group 1:
Compare the mass of the 5 objects by estimating.
Arrange them from the lightest to the heaviest.
Group 2:
Compare their mass. Use a balance scale.
Arrange them from the lightest to the heaviest.
Group 3:
Compare their mass by estimating.
Arrange them from the heaviest to the lightest.
Group 4:
Compare their mass. Use a balance scale.
Arrange them from the heaviest to the lightest.
| LO 4.6 |
4 ____ ; 7 ____ ; 9 ____ ; 8 ____ ; 6 ____
| LO 1.10 |
| 1 | 5 | ||||||||
| 20 | |||||||||
| 22 | |||||||||
| 38 | |||||||||
| 50 |
- Count to 20 and back to 0.
- Count to 30 and back to 0.
- Count to 40 and back to 0.
- Count to 50 and back to 0.

| LO 1.1 | LO 1.3 | LO 2.2 |
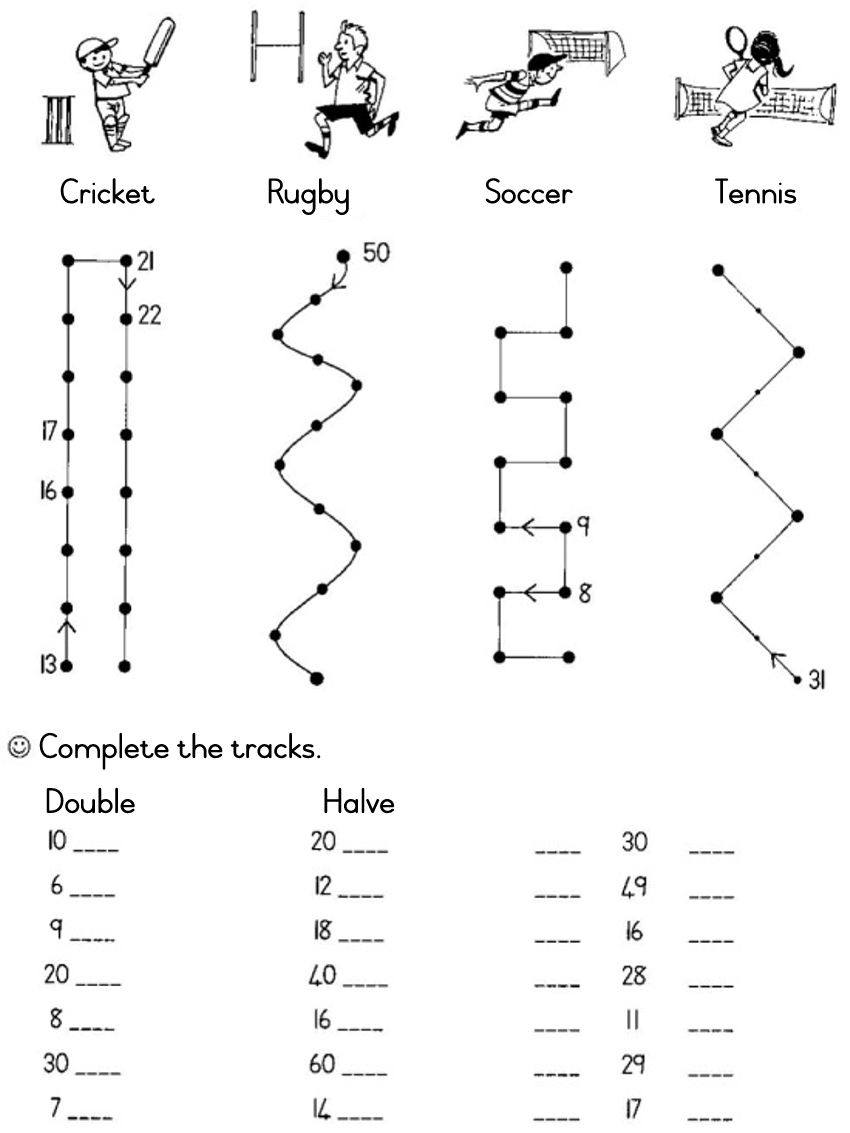
| LO 1.10 | LO 2.2 |
Henry made __________ runs.
Write the number sentence; 8 + ____________________.
They scored _________ points.
Write the number sentence; _______________________.
She played __________ games of tennis.
Write the number sentence; _______________________.
Pat’s team scored ____________ goals.
The ‘B’ soccer scored __________ goals.
Write the number sentence __________________.
| LO 1.9 |
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.1: We know this when the learner counts to at least 100 everyday objects reliably;
Assessment Standard 1.3: We know this when the learner knows and reads number symbols from 1 to at least 200 and writes number names from 1 to at least 100;
Assessment Standard 1.9: We know this when the learner performs mental calculations involving:
1.9.1 addition and subtraction for numbers to at least 20;
1.9.2 multiplication of whole numbers with solutions to at least 20.
Assessment Standard 1.10: We know this when the learner uses the following techniques:
1.10.1 building up and breaking down numbers;
1.10.2 doubling and halving;
1.10.3 using concrete apparatus (e.g. counters);
1.10.4 number-lines;
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.2: We know this when the learner copies and extends simple number sequences to at least 200.
Learning Outcome 4: The learner will be able to use appropriate measuring units, instruments and formulae in a variety of contexts.
Assessment Standard 4.6: We know this when the learner estimates, measures, compares and orders three-dimensional objects using non-standard measures.

Notification Switch
Would you like to follow the 'Mathematics grade 2' conversation and receive update notifications?