| << Chapter < Page | Chapter >> Page > |
Count in tens regularly, forwards and backwards, from any number.
E.g. 4 14 24 34 44 54 64 74 84 94
97 87 77 67 57 47 37 27 17 7
The learners should be aware of how important the number 10 is in our number system (decimal system).
They should know the combinations of 10 very well and must be tested regularly. Much practice is required.

A: ______________________________ ______________________________
B: ______________________________ ______________________________
C: ______________________________ ______________________________
D: ______________________________ ______________________________
E: ______________________________
______________________________
F: ______________________________
______________________________
G: ______________________________
______________________________
H: ______________________________
| LO 1.3 |
Which numbers come under 5 and 9 ?
5 : 15 ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; 95
9 ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; 99
3 ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; 93
93 ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; _____ ; 3
| LO 1.11 |
Bonny and Tommy have made these “tens bugs”.

3 + 7 = 10 7 + 3 = 10

7 and 3
____ and 9
____ and 5
3 and 7
9 and ____
5 and ____
____ and 8
____ and 6
8 and ____
6 and ____
Let’s say that 10 ’s 3 breaks off, then 7 remains.
Number sentence: 10 - 3 = 7
If 10 ’s 7 breaks off, then 3 remains.
Number sentence: 10 - 7 = 3

Always think of the two parts!
| LO 1.8 |
 |
|||||
| Total: | |||||
| Do these: | |||||
 |
|||||
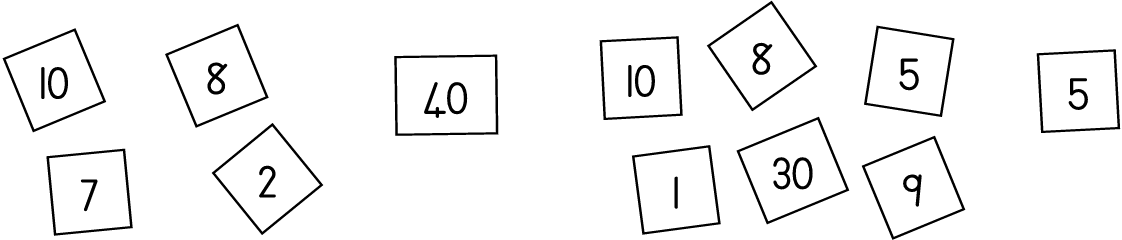 |
|||||

| LO 1.8 |
Complete the patterns.

Complete these patterns.

| LO 2.2 |
Divide 30 smarties among Bonny and Tommy and their friend, Terry, so that they all get the same number. How many smarties will each one get?
| LO 1.7 |
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.3: We know this when the learner knows, reads and writes number symbols and names from 1 to at least 1 000;
Assessment Standard 1.7: We know this when the learner solves and explains solutions to practical problems that involve equal sharing and grouping and that lead to solutions that also include unitary and nonunitary fractions (e.g. 1¼1 , ¾4);
Assessment Standard 1.8: We know this when the learner can perform calculations, using appropriate symbols, to solve problems involving:
1.8.1 addition and subtraction of whole numbers with at least 3 digits;
1.8.2 multiplication of at least whole 2-digit by 1-digit numbers;
1.8.3 division of at least whole 2-digit by 1-digit numbers;
Assessment Standard 1.9: We know this when the learner performs mental calculations involving:
1.9.1 addition and subtraction for numbers to at least 50;
1.9.2 multiplication of whole numbers with solutions to at least 50;
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.2: We know this when the learner copies and extends simple number sequences to at least 1 000.

Notification Switch
Would you like to follow the 'Mathematics grade 3' conversation and receive update notifications?