| << Chapter < Page | Chapter >> Page > |
Mathematically, analog signals are functions having as their independent variables continuous quantities, such as space andtime. Discrete-time signals are functions defined on the integers; they are sequences. As with analog signals, we seekways of decomposing discrete-time signals into simpler components. Because this approach leads to a betterunderstanding of signal structure, we can exploit that structure to represent information (create ways of representinginformation with signals) and to extract information (retrieve the information thus represented). For symbolic-valued signals,the approach is different: We develop a common representation of all symbolic-valued signals so that we can embody theinformation they contain in a unified way. From an information representation perspective, the most important issue becomes,for both real-valued and symbolic-valued signals, efficiency: what is the most parsimonious and compact way to representinformation so that it can be extracted later.
A discrete-time signal is represented symbolically as
, where
.
Cosine
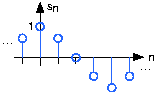
The most important signal is, of course, the complex exponential sequence .
Discrete-time sinusoids have the obvious form . As opposed to analog complex exponentials and sinusoids that can have their frequencies be any real value,frequencies of their discrete-time counterparts yield unique waveforms only when lies in the interval . This choice of frequency interval is arbitrary; we can also choose the frequency to lie in the interval . How to choose a unit-length interval for a sinusoid's frequency will become evident later.
The second-most important discrete-time signal is the unit sample , which is defined to be

The unit step in discrete-time is well-defined at the origin, as opposed to the situation with analog signals.
An interesting aspect of discrete-time signals is that their values do not need to be real numbers. We do have real-valueddiscrete-time signals like the sinusoid, but we also have signals that denote the sequence of characters typed on thekeyboard. Such characters certainly aren't real numbers, and as a collection of possible signal values, they have littlemathematical structure other than that they are members of a set. More formally, each element of the symbolic-valued signal takes on one of the values which comprise the alphabet . This technical terminology does not mean we restrict symbols to being members of the Englishor Greek alphabet. They could represent keyboard characters, bytes (8-bit quantities), integers that convey dailytemperature. Whether controlled by software or not, discrete-time systems are ultimately constructed from digitalcircuits, which consist entirely of analog circuit elements. Furthermore, the transmission andreception of discrete-time signals, like e-mail, is accomplished with analog signals and systems. Understandinghow discrete-time and analog signals and systems intertwine is perhaps the main goal of this course.
Discrete-time systems can act on discrete-time signals in ways similar to those found in analog signals and systems. Becauseof the role of software in discrete-time systems, many more different systems can be envisioned and "constructed" withprograms than can be with analog signals. In fact, a special class of analog signals can be converted into discrete-timesignals, processed with software, and converted back into an analog signal, all without the incursion of error. For suchsignals, systems can be easily produced in software, with equivalent analog realizations difficult, if not impossible,to design.

Notification Switch
Would you like to follow the 'Fundamentals of electrical engineering i' conversation and receive update notifications?