| << Chapter < Page | Chapter >> Page > |
Before looking at this module, hopefully you have an idea of what a signal is and what basic classifications and properties a signal canhave. In review, a signal is a function defined with respect to an independent variable. This variable is often timebut could represent any number of things. Mathematically, continuous time analogsignals have continuous independent and dependent variables. This module will describe some useful continuous time analog signals.
One of the most important elemental signal that you will deal with is the real-valued sinusoid. In its continuous-timeform, we write the general expression as

As important as the general sinusoid, the complex exponential function will become a critical part of your study of signals and systems. Its general continuous form iswritten as
The unit impulse function, also known asthe Dirac delta function, is a signal that has infinite height andinfinitesimal width. However, because of the way it is defined, it integrates to one. While this signal is useful for theunderstanding of many concepts, a formal understanding of its definition more involved. The unit impulse is commonly denoted .
More detail is provided in the section on the continuous time impulse function. For now, it suffices to say that this signal is crucially important in the study of continuous signals, as it allows the sifting property to be used in signal representation and signal decomposition.
Another very basic signal is the unit-step function that is defined as
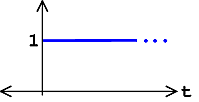
The step function is a useful tool for testing and for defining other signals. For example, whendifferent shifted versions of the step function are multiplied by other signals, one can select a certain portion of thesignal and zero out the rest.
Some of the most important and most frequently encountered signals have been discussed in this module. There are, of course, many other signals of significant consequence not discussed here. As you will see later, many of the other more complicated signals will be studied in terms of those listed here. Especially take note of the complex exponentials and unit impulse functions, which will be the key focus of several topics included in this course.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?