| << Chapter < Page | Chapter >> Page > |
Next, we'll derive the FT of some basic continuous-time signals. [link] summarizes these transform pairs.
Let's begin with the rectangular pulse
The pulse function, is shown in [link] . Evaluating the Fourier transform integral with gives
A plot of is shown in [link] .
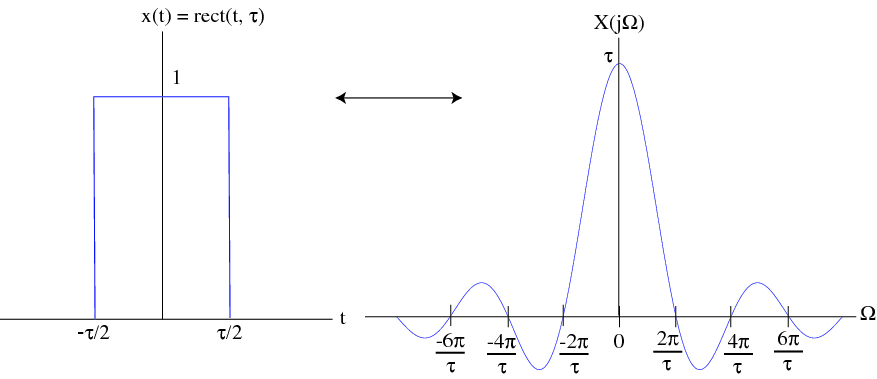
Note that when , . We now have the following transform pair:
The unit impulse function was described in a previous section. From the sifting property of the impulse function we find that
or
The complex exponential function, , has a Fourier transform which is difficult to evaluate directly. It is easier to start with the Fourier transform itself and work backwards using the inverse Fourier transform. Suppose we want to find the time-domain signal which has Fourier transform . We can begin by using the inverse Fourier transform [link]
This result follows from the sifting property of the impulse function. By linearity, we can then write
The cosine signal can be expressed in terms of complex exponentials using Euler's Identity
Applying linearity and the Fourier transform of complex exponentials to the right side of [link] , we quickly get:
The real exponential function is given by , where . To find its FT, we start with the definition
therefore,
In a previous section, we looked at the unit step function,
A closely related signal is the signum function, defined by
from which it follows that
The signum function can be described as follows:
Since we already have the Fourier transform of the exponential signal,
Using [link] and linearity then leads to
| 1 | |
When working problems involving finding the Fourier transform, it is often preferable to use a table of transform pairs rather than to recalculate the Fourier transform from scratch. Often, transform pairs in can be combined with known Fourier transform properties to find new Fourier transforms.
Example 3.1 Find the Fourier transform of: . Clearly, we can write where . Therefore, we can combine the known transform of from [link] , namely,
with the time reversal property:
to get the answer:

Notification Switch
Would you like to follow the 'Signals, systems, and society' conversation and receive update notifications?