| << Chapter < Page | Chapter >> Page > |
What are the amplitude, period, and phase shift for the function?
amplitude: 8,000; period: 10; phase shift: 0
Over this domain, when does the population reach 18,000? 13,000?
What is the predicted population in 2007? 2010?
In 2007, the predicted population is 4,413. In 2010, the population will be 11,924.
For the following exercises, suppose a weight is attached to a spring and bobs up and down, exhibiting symmetry.
Suppose the graph of the displacement function is shown in [link] , where the values on the x -axis represent the time in seconds and the y -axis represents the displacement in inches. Give the equation that models the vertical displacement of the weight on the spring.
![A graph of a consine function over one period. Graphed on the domain of [0,10]. Range is [-5,5].](/ocw/mirror/col11758/m49390/CNX_Precalc_Figure_06_03_225.jpg)
At what time does the displacement from the equilibrium point equal zero?
What is the time required for the weight to return to its initial height of 5 inches? In other words, what is the period for the displacement function?
10 seconds
For the following exercises, find the exact value without the aid of a calculator.
Graph and on the interval and explain any observations.
The graphs are not symmetrical with respect to the line
They are symmetrical with respect to the
-axis.
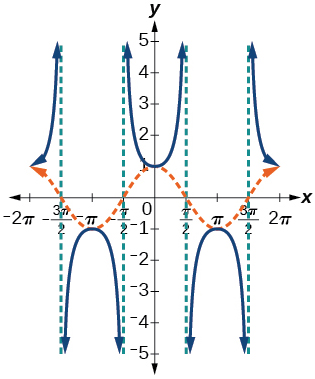
Graph and and explain any observations.
Graph the function on the interval and compare the graph to the graph of on the same interval. Describe any observations.
The graphs appear to be identical.
![Two graphs of two identical functions on the interval [-1 to 1]. Both graphs appear sinusoidal.](/ocw/mirror/col11758/m49390/CNX_Precalc_Figure_06_03_228.jpg)
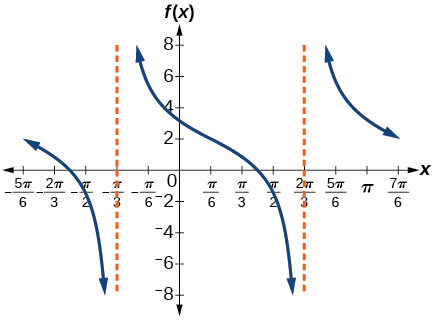
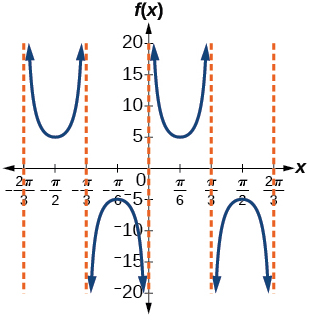
For the following exercises, sketch the graph of each function for two full periods. Determine the amplitude, the period, and the equation for the midline.
amplitude: none; period:
midline:
asymptotes:
where
is an integer
amplitude: none; period:
midline:
asymptotes:
where
is an integer
For the following exercises, determine the amplitude, period, and midline of the graph, and then find a formula for the function.
Give in terms of a sine function.
![A graph of two periods of a sine function, graphed from -2 to 2. Range is [-6,-2], period is 2, and amplitude is 2.](/ocw/mirror/col11758/m49390/CNX_Precalc_Figure_06_03_242.jpg)
Give in terms of a sine function.
![A graph of two periods of a sine function, graphed over -2 to 2. Range is [-2,2], period is 2, and amplitude is 2.](/ocw/mirror/col11758/m49390/CNX_Precalc_Figure_06_03_243.jpg)
amplitude: 2; period: 2; midline:
Give in terms of a tangent function.

For the following exercises, find the amplitude, period, phase shift, and midline.
The outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is 68°F at midnight and the high and low temperatures during the day are 80°F and 56°F, respectively. Assuming is the number of hours since midnight, find a function for the temperature, in terms of
Water is pumped into a storage bin and empties according to a periodic rate. The depth of the water is 3 feet at its lowest at 2:00 a.m. and 71 feet at its highest, which occurs every 5 hours. Write a cosine function that models the depth of the water as a function of time, and then graph the function for one period.
For the following exercises, find the period and horizontal shift of each function.
Write the equation for the graph in [link] in terms of the secant function and give the period and phase shift.
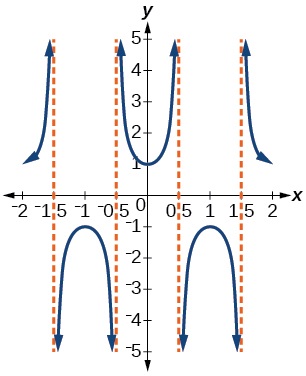
period: 2; phase shift: 0
For the following exercises, graph the functions on the specified window and answer the questions.
Graph on the viewing window by Approximate the graph’s period.
Graph on the following domains in and Suppose this function models sound waves. Why would these views look so different?
The views are different because the period of the wave is Over a bigger domain, there will be more cycles of the graph.
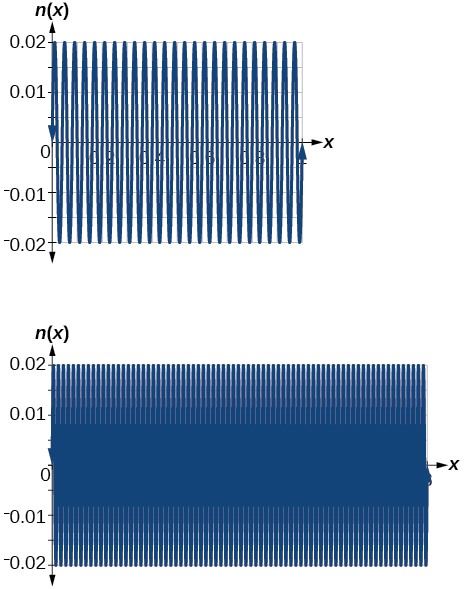
Graph on and explain any observations.
For the following exercises, let
What is the smallest possible value for
Where is the function increasing on the interval
On the approximate intervals
For the following exercises, find and graph one period of the periodic function with the given amplitude, period, and phase shift.
Sine curve with amplitude 3, period and phase shift
For the following exercises, graph the function. Describe the graph and, wherever applicable, any periodic behavior, amplitude, asymptotes, or undefined points.
For the following exercises, find the exact value.
For the following exercises, suppose
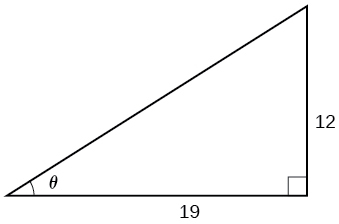
Given [link] , find the measure of angle to three decimal places. Answer in radians.
For the following exercises, determine whether the equation is true or false.
The grade of a road is 7%. This means that for every horizontal distance of 100 feet on the road, the vertical rise is 7 feet. Find the angle the road makes with the horizontal in radians.
approximately 0.07 radians

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?