| << Chapter < Page | Chapter >> Page > |
Note: Answers to the Cumulative Review can be found in the Supplemental Resources. Please visit http://openstaxcollege.org to view an updated list of the Learning Resources for this title and how to access them.
No exercises.
Simplify:
Solve:
Translate into an algebraic expression.
less than the product of and
Translate into an algebraic equation and solve.
Twice the difference of and gives
Find all the factors of
Find the prime factorization of
Find the least common multiple of and
Simplify:
Translate into an algebraic expression or equation.
The sum of and increased by
The product of
The quotient of and the sum of
The product of and is
Solve:
Locate the numbers on a number line.
Simplify:
Simplify:
Write in order from smallest to largest:
Solve :
Using as the estimate for pi, approximate the (a) circumference and (b) area of a circle whose radius is inches.
Find the mean of the numbers,
Find the median of the numbers,
Identify the mode of the numbers,
Find the unit price of one t-shirt if they are sold at for
Convert to (a) a fraction and (b) a decimal.
Translate and solve.
is of what number?
The nutrition label on a package of granola bars says that each granola bar has calories, and calories are from fat. What percent of the total calories is from fat?
Elliot received commission when he sold a painting at the art gallery where he works. What was the rate of commission?
Nandita bought a set of towels on sale for The original price of the towels was What was the discount rate?
Alan invested in a friend’s business. In years the friend paid him the plus interest. What was the rate of interest?
Solve:
List the (a) whole numbers, (b) integers, (c) rational numbers, (d) irrational numbers,
(e) real numbers
Simplify:
A playground is feet wide. Convert the width to yards.
Every day last week Amit recorded the number of minutes he spent reading. The recorded number of minutes he read each day was How many hours did Amit spend reading last week?
June walked kilometers. Convert this length to miles knowing mile is kilometer.
Solve:
Translate and solve.
Four less than is
One number is less than another. Their sum is negative twenty-two. Find the numbers.
The sum of two consecutive integers is Find the numbers.
Wilma has in dimes and quarters. The number of dimes is less than the number of quarters. How many of each coin does she have?
Two angles are supplementary. The larger angle is more than the smaller angle. Find the measurements of both angles.
One angle of a triangle is more than the smallest angle. The largest angle is the sum of the other angles. Find the measurements of all three angles.
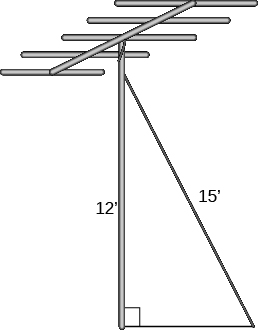
Erik needs to attach a wire to hold the antenna to the roof of his house, as shown in the figure. The antenna is feet tall and Erik has feet of wire. How far from the base of the antenna can he attach the wire?
The width of a rectangle is less than the length. The perimeter is inches. Find the length and the width.
Find the (a) volume and (b) surface area of a rectangular carton with length inches, width inches, and height inches.
Simplify:
Write in scientific notation:
Factor the greatest common factor from the polynomial.
Graph:
Find the intercepts.
Graph using the intercepts.
Find slope.
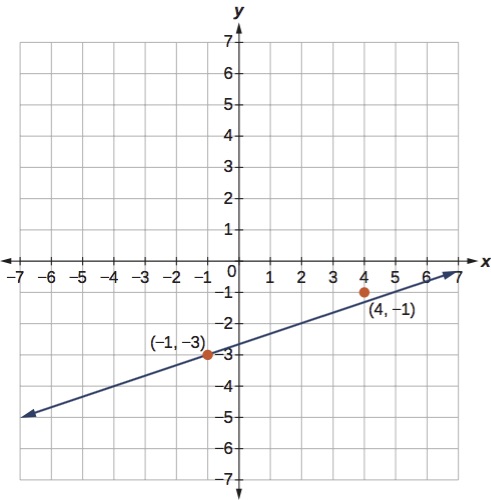
Use the slope formula to find the slope of the line between the points
Graph the line passing through the point and with slope

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?