| << Chapter < Page | Chapter >> Page > |
In digital communications filters are important in the process of upsampling. Upsampling is required for transmission because we want the signal's frequency representation to be narrow and confined to frequencies around the carrier frequency. By upsampling the signal, the frequency response of the signal to be transmitted gets compressed and becomes band limited to a significantly smaller range of frequencies, which is necessary for transmission.

As can be seen from the figure above, (a) shows the frequency domain representation of the signal to be transmitted, (b) shows the upsampled version of the frequency response, and upon low pass filtering the upsampled signal we get only two spikes. When the signal is modulated to the carrier frequency, both spikes appear at the corresponding carrier frequency in (c). This is important because we don't want information to be spread across the frequency spectrum, rather we want to transmit the signal at a specific carrier frequency.
The upsampling process is accomplished by taking a signal, inserting L zeros between each sample and then low pass filtering the result. Below is a description of possible low pass filters that can be used to achieve this result.
The raised cosine filter is a type of low pass filter that accomplishes the interpolation necessary after inserting the L zeros between each sample. It's frequency response is given by:

In the filter α is a parameter which is between 0 and 1 and is called the rolloff factor. The larger α is, the wider the bandwidth of the filter. As α approaches zero the filter will become a brick wall and will look like a box in the frequency domain. The Impulse response of the filter is shown in the figure below:

As can be seen above, the time domain representation is given by a sinc and so in reality the raised cosine filter would extend to plus and minus infinity. However, above the impulse response was truncated and selected to have a length of 41 for the purposes of our digital communication scheme. The raised cosine filter is the best filter for digital communication, specifically 16 QAM, because it removes interference that may occur from one symbol to the next. This means that the waveform can be recovered perfectly at the receiver and this is why the raised cosine filter is typically used in digital communication.
In order to complete the upsampling process it is necessary to convolve the impulse response of the raised cosine filter and the vector that contains the signal with zeros inserted between the samples. The output of this convolution will be the upsampled signal. Below is the output of the real part of a [1 0 1 0] sequence convolved with the raised cosine filter.

As can be seen above, the absolute value of the maximum value is -3. This is because the first two bits, [1 0] correspond to the real part of the sequence and they get mapped to a value of I=-3. Below is the imaginary part of the signal, and as we can see the absolute value of the maximum value is 1. This is because the last to bits, [1 0]correspond to the imaginary part of the sequence and they get mapped to a value of Q=1.

The raised cosine filter is used because it limits the bandwidth of the signal and decays quickly in the time domain. The advantages of this is that it allows for data transmission in specific frequency ranges with an insignificant amount of information spread out across large frequencies.
Butterworth filters are another type of low pass filter which can be used to complete the upsampling process. The frequency response of the Butterworth filter is given by:
Where N is a parameter which is called the order of the filter and ω c is the cutoff frequency. The Butterworth filter acts like a low pass filter because it has a flat frequency response that is usually unity gain in the passband and gradually rolls off to zero in the stopband. In between the passband and the stop band we have the cutoff frequency which will occur at the point where the gain is equal to 0.707 (1/sqrt(2)). Butterworth filters have a relatively slow roll off, especially when compared to the raised cosine filter. Below is the impulse response of the Butterworth filter:

Given a sequence of [1 0 1 0] the output of the low pass filtering of the real part of the signal will be:
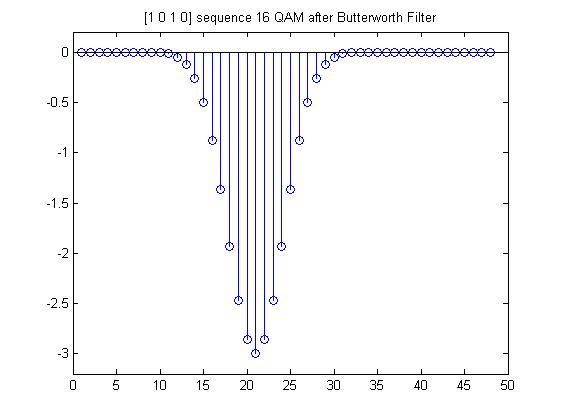
The output of low pass filtering the imaginary part of the signal with a Butterworth filter will be:

As can be seen the output of the Butterworth filter is similar to that of the raised cosine filter, where both map the real part of the sequence to -3 and the imaginary part of the sequence to 1. The main difference is that the raised cosine filter's output has ripples extending on both sides, while the Butterworth filter does not. This means that the Butterworth filter's output does not need to be truncated since it does not extend to infinity like the output of the raised cosine filter does. The output of these filters would then be modulated appropriately as described, summed together and then transmitted through the channel as described in the QAM module.

Notification Switch
Would you like to follow the 'Digital filters in 16-qam communication' conversation and receive update notifications?