| << Chapter < Page | Chapter >> Page > |
INTRODUCTION
The learning programme for grade six consists of five modules:
1. Number concept, Addition and Subtraction
2. Multiplication and Division
3. Fractions and Decimal fractions
4. Measurement and Time
5. Geometry; Data handling and Probability
COMMON AND DECIMAL FRACTIONS (LO 1; 2 AND 5)
LEARNING UNIT 1 FOCUSES ON COMMON FRACTIONS
1.1 402
1.2 312
1.2 695
1.4 665
1.5 1,236
1.6 1,5
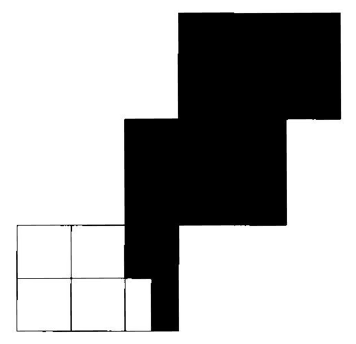
1.1
1.2 >1
2.
2.1
2.2
2.3
2.4
3.
3.1
3.2 3.4
3.3
1. Calculate this on your own:
1.1 of 670
.......................................................................
.......................................................................
.......................................................................
.......................................................................
1.2 of 526
.......................................................................
.......................................................................
.......................................................................
.......................................................................
1.3 of 834
.......................................................................
.......................................................................
.......................................................................
.......................................................................
1.4 of 1 064
.......................................................................
.......................................................................
.......................................................................
.......................................................................
1.5 of 1,648 m
.......................................................................
.......................................................................
.......................................................................
.......................................................................
1.6 of 2,7kℓ
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.8: We know this when the learner estimates and calculates by selecting and using operations appropriate to solving problems that involve:
1.8.6 finding fractions of whole numbers.

Notification Switch
Would you like to follow the 'Mathematics grade 6' conversation and receive update notifications?