| << Chapter < Page | Chapter >> Page > |

5 Puntediagramme
Die toetspunte in Skeinat en Wiskunde van ’n groep van 22 leerders word in hierdie tabel weergegee.
| Leerder: | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V |
| Skeinat | 75 | 45 | 28 | 66 | 58 | 81 | 23 | 69 | 60 | 48 | 72 | 37 | 47 | 90 | 57 | 88 | 45 | 56 | 62 | 40 | 53 | 48 |
| Wiskunde | 65 | 31 | 40 | 67 | 52 | 75 | 34 | 95 | 70 | 66 | 58 | 40 | 45 | 84 | 75 | 70 | 55 | 61 | 53 | 55 | 72 | 49 |
Die puntediagram van die punte:
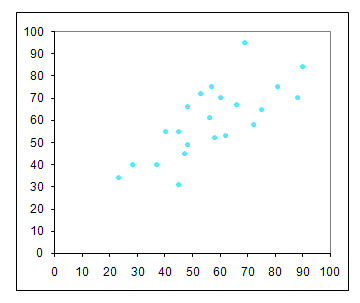
Elke leerling word voorgestel deur ’n punt met koördinate (Skeinat-punt ; Wiskunde-punt). Leerder A is (75;65). Soek daardie punt. Leerder B is (45;31), ens. Die grafiekblokkies is uitgelaat om die grafiek duideliker te maak.
As die punte ’n patroon vorm, soos dié, ongeveer vanaf die hoek onder links na bo regs, beteken dit dat daar ’n verband is tussen die leerders se punte vir die twee vakke.
| LU 2 |
| Patrone, Funksies en AlgebraDie leerder is in staat om patrone en verwantskappe te herken, te beskryf en voor te stel, en probleme op te los deur algebraïese taal en vaardighede te gebruik. |
| Dit is duidelik wanneer die leerder: |
| 2.1 op verskillende maniere ‘n verskeidenheid numeriese en meetkundige patrone en verwantskappe ondersoek deur dit voor te stel en te veralgemeen, en deur die reëls onderliggend daaraan te verduidelik en te bewys (insluitend patrone in natuurlike en kulturele vorms, en patrone wat die leerder self geskep het); |
| 2.2 voorstellings maak van verwantskappe tussen veranderlikes en dit gebruik sodat invoer– en/of uitvoerwaardes op ‘n verskeidenheid maniere bepaal kan word deur die gebruik van: |
| 2.2.1 woordelikse beskrywings;2.2.2 vloeidiagramme;2.2.3 tabelle;2.2.4 formules en vergelykings; |
| 2.3 wiskundige modelle saamstel wat oplossings vir probleemsituasies voorstel, beskryf en voorsien, en verantwoordelikheid toon teenoor die omgewing en die gesondheid van ander (insluitend probleme binne menseregte-, sosiale, ekonomiese, kulturele en omgewingskontekste); |
| 2.4 vergelykings oplos deur inspeksie, deur ‘n proses van probeer–en–verbeter of algebraïese prosesse (optellings- en vermenigvuldigngsomgekeerdes, asook faktorisering) en die oplossings kontroleer deur vervanging; |
| 2.5 grafieke op die Cartesiese vlak teken vir gegewe vergelykings (met twee veranderlikes), of die vergelykings of formules bepaal van gegewe grafieke, deur, waar nodig, van tabelle gebruik te maak; |
| 2.6 die ekwivalensie van verskillende beskrywings van dieselfde verwantskap of reël bepaal, ontleed en interpreteer, wat soos volg voorgestel word: |
2.6.1 woordeliks;2.6.2 in vloeidiagramme;2.6.3 in tabelle;2.6.4 deur vergelykings of uitdrukkings;
|
| LU 5 |
| DatahanteringDie leerder is in staat om data te versamel, op te som, voor te stel en krities te ontleed om gevolgtrekkings en voorspellings te maak en om toevallige variasie te interpreteer en te bepaal. |
| Dit is duidelik wanneer die leerder: |
| 5.1 vrae stel oor menseregte-, sosiale, politieke, omgewings– en ekonomiese sake in Suid–Afrika; |
| 5.2 geskikte metodes kies, staaf en gebruik vir die versameling van data(alleen en/of as lid van ‘n groep of span), insluitend vraelyste, onderhoude, eksperimente en bronne soos boeke, tydskrifte en die Internet, om vrae te beantwoord en gevolgtrekkings en voorspellings oor die omgewing te maak; |
| 5.3 numeriese data op verskillende maniere organiseer ten einde ‘n opsomming te maak deur die volgende vas te stel: |
| 5.3.1 bepalers van sentrale neiging; |
| 5.3.2 bepalers van verspreiding; |
| 5.4 ‘n verskeidenheid grafieke met die hand of met behulp van tegnologie teken om data voor te stel en te interpreteer, insluitend: |
| 5.4.1 staafgrafieke en dubbele staafgrafieke; |
| 5.4.2 histogramme met gegewe en eie intervalle; |
| 5.4.3 sirkeldiagramme; |
| 5.4.4 lyn– en gebroke lyngrafieke; |
| 5.4.5 verspreidingsgrafieke; |

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?