| << Chapter < Page | Chapter >> Page > |
If is the region bounded by the graphs of the functions and over the interval find the area of region
units 2
In [link] , we defined the interval of interest as part of the problem statement. Quite often, though, we want to define our interval of interest based on where the graphs of the two functions intersect. This is illustrated in the following example.
If is the region bounded above by the graph of the function and below by the graph of the function find the area of region
The region is depicted in the following figure.

We first need to compute where the graphs of the functions intersect. Setting we get
The graphs of the functions intersect when or so we want to integrate from to Since for we obtain
The area of the region is units 2 .
If R is the region bounded above by the graph of the function and below by the graph of the function find the area of region
unit 2
So far, we have required over the entire interval of interest, but what if we want to look at regions bounded by the graphs of functions that cross one another? In that case, we modify the process we just developed by using the absolute value function.
Let and be continuous functions over an interval Let denote the region between the graphs of and and be bounded on the left and right by the lines and respectively. Then, the area of is given by
In practice, applying this theorem requires us to break up the interval and evaluate several integrals, depending on which of the function values is greater over a given part of the interval. We study this process in the following example.
If R is the region between the graphs of the functions and over the interval find the area of region
The region is depicted in the following figure.
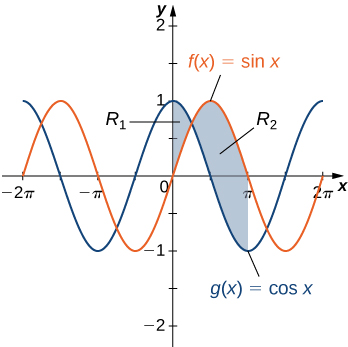
The graphs of the functions intersect at For so
On the other hand, for so
Then
The area of the region is units 2 .
If R is the region between the graphs of the functions and over the interval find the area of region
units 2
Consider the region depicted in [link] . Find the area of
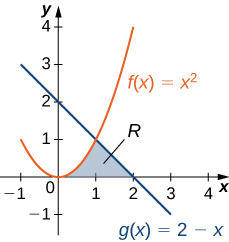
As with [link] , we need to divide the interval into two pieces. The graphs of the functions intersect at (set and solve for x ), so we evaluate two separate integrals: one over the interval and one over the interval
Over the interval the region is bounded above by and below by the x -axis, so we have
Over the interval the region is bounded above by and below by the so we have
Adding these areas together, we obtain
The area of the region is units 2 .

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?