6.7 Stokes’ theorem

By Clairaut’s theorem, $\frac{{\partial }^{2}z}{\partial x\partial y}=\frac{{\partial }^{2}z}{\partial y\partial x}.$ Therefore, four of the terms disappear from this double integral, and we are left with

which equals ${\displaystyle \underset{S}{\iint }\text{curl}\text{F}·d\text{S}.}$

□

We have shown that Stokes’ theorem is true in the case of a function with a domain that is a simply connected region of finite area. We can quickly confirm this theorem for another important case: when vector field F is conservative. If F is conservative, the curl of F is zero, so ${\displaystyle \underset{S}{\iint }\text{curl}\text{F}·d\text{S}=0.}$ Since the boundary of S is a closed curve, ${\displaystyle {\int }_C\text{F}·d\text{r}}$ is also zero.

Verifying stokes’ theorem for a specific case

Verify that Stokes’ theorem is true for vector field $\text{F}\left(x,y\right)=⟨\text{−}z,x,0⟩$ and surface S , where S is the hemisphere, oriented outward, with parameterization

$\text{r}(\varphi ,\theta )=⟨\text{sin}\varphi \text{cos}\theta ,\text{sin}\varphi \text{sin}\theta ,\text{cos}\varphi ⟩,0\le \theta \le \pi ,0\le \varphi \le \pi$ as shown in the following figure.

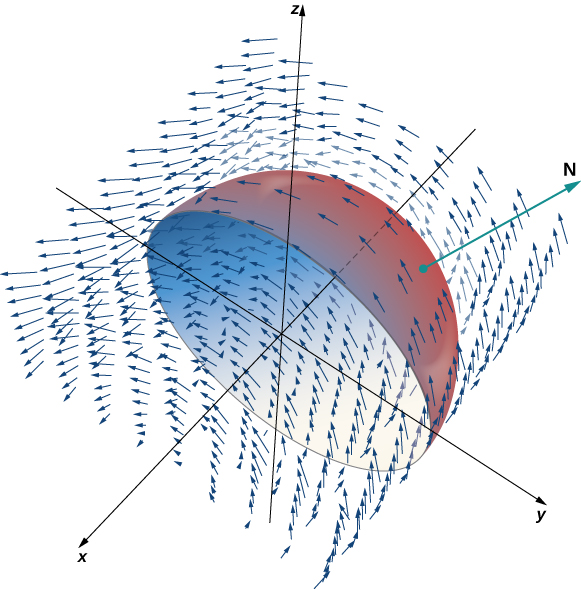
Let C be the boundary of S. Note that C is a circle of radius 1, centered at the origin, sitting in plane $y=0.$ This circle has parameterization $⟨\text{cos}t,0,\text{sin}t⟩,0\le t\le 2\pi .$ By [link] ,

$\begin{array}{cc}\hfill {\displaystyle {\int }_C\text{F}·d\text{r}}& ={\displaystyle {\int }_0^{2\pi }⟨\text{−}\text{sin}t,\text{cos}t,0⟩·⟨\text{−}\text{sin}t,0,\text{cos}t⟩}dt\hfill \\ & ={\displaystyle {\int }_0^{2\pi }{\text{sin}}^{2}t}dt=\pi .\hfill \end{array}$

By [link] ,

$\begin{array}{cc}\hfill {\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}}& ={\displaystyle {\iint }_D\text{curl}\text{F}\left(\text{r}\left(\varphi ,\theta \right)\right)}·\left({\text{t}}_{\varphi }\times {\text{t}}_{\theta }\right)dA\hfill \\ & ={\displaystyle {\iint }_D⟨0,\mathrm{-1},1⟩·⟨\text{cos}\theta {\text{sin}}^2\varphi ,\text{sin}\theta {\text{sin}}^2\varphi ,\text{sin}\varphi \text{cos}\varphi ⟩dA}\hfill \\ & ={\displaystyle {\int }_0^{\pi }{\displaystyle {\int }_0^{\pi }\left(\text{sin}\varphi \text{cos}\varphi -\text{sin}\theta {\text{sin}}^2\varphi \right)}}d\varphi d\theta \hfill \\ & =\frac{\pi }{2}{\displaystyle {\int }_0^{\pi }\text{sin}\theta d\theta }=\pi .\hfill \end{array}$

Therefore, we have verified Stokes’ theorem for this example.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Applying stokes’ theorem

Stokes’ theorem translates between the flux integral of surface S to a line integral around the boundary of S . Therefore, the theorem allows us to compute surface integrals or line integrals that would ordinarily be quite difficult by translating the line integral into a surface integral or vice versa. We now study some examples of each kind of translation.

Calculating a surface integral

Calculate surface integral ${\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}},$ where S is the surface, oriented outward, in [link] and $\text{F}=⟨z,2xy,x+y⟩.$

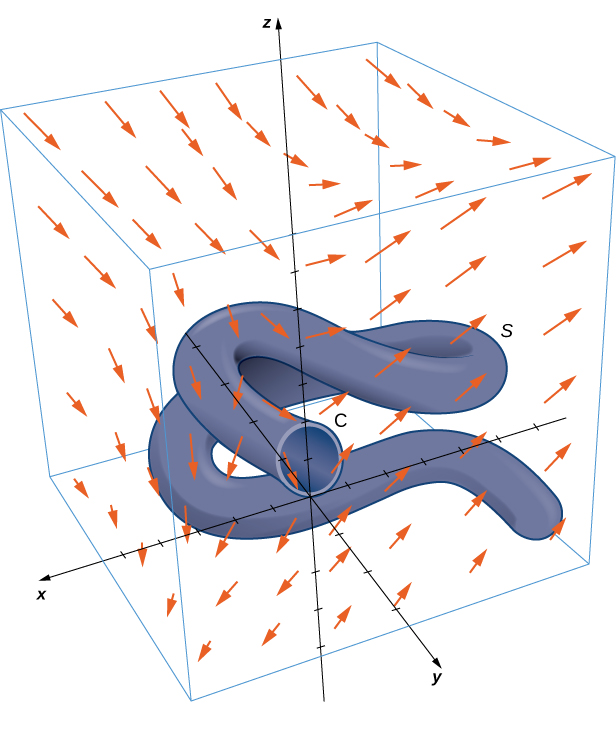
Note that to calculate ${\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}}$ without using Stokes’ theorem, we would need to use [link] . Use of this equation requires a parameterization of S . Surface S is complicated enough that it would be extremely difficult to find a parameterization. Therefore, the methods we have learned in previous sections are not useful for this problem. Instead, we use Stokes’ theorem, noting that the boundary C of the surface is merely a single circle with radius 1.

The curl of F is $⟨1,1,2y⟩.$ By Stokes’ theorem,

${\displaystyle {\iint }_S\text{curl}\text{F}·d\text{S}}={\displaystyle {\int }_C\text{F}·d\text{r},}$

where C has parameterization $⟨\text{cos}t,\text{sin}t,1⟩,0\le t<2\pi .$ By [link] ,

$\begin{array}{cc}\hfill {\displaystyle {\iint }_S\text{curl}\text{F}}·d\text{S}& ={\displaystyle {\int }_C\text{F}·d\text{r}}\hfill \\ & ={\displaystyle {\int }_0^{2\pi }⟨1,2\text{sin}t\text{cos}t,\text{cos}t+\text{sin}t⟩·⟨\text{−}\text{sin}t,\text{cos}t,0⟩dt}\hfill \\ & ={\displaystyle {\int }_0^{2\pi }\left(\text{−}\text{sin}t+2\text{sin}t{\text{cos}}^{2}t\right)dt}\hfill \\ & ={\left[\text{cos}t-\frac{2{\text{cos}}^{3}t}{3}\right]}_0^{2\pi }\hfill \\ & =\text{cos}(2\pi )-\frac{2{\text{cos}}^3(2\pi )}{3}-\left(\text{cos}(0)-\frac{2{\text{cos}}^3(0)}{3}\right)\hfill \\ & =0.\hfill \end{array}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!