| << Chapter < Page | Chapter >> Page > |
The Z transform is a generalization of the Discrete-Time Fourier Transform . It is used because the DTFT does not converge/exist for many important signals, and yet does for the z-transform. It is also used because it is notationally cleaner than the DTFT. In contrast to the DTFT, instead of using complex exponentials of the form , with purely imaginary parameters, the Z transform uses the more general, , where is complex. The Z-transform thus allows one to bring in the power of complex variable theory into Digital Signal Processing.
Although Z transforms are rarely solved in practice using integration
(
tables and
computers (
Taking a look at the equations describing the Z-Transform and the Discrete-Time Fourier Transform:
With the DTFT, we have a complex-valued function of a real-valued variable
(and 2
periodic).
The Z-transform is a complex-valued function of a complex valued variable z.
Plots

With the Fourier transform, we had a complex-valued function of a purely imaginary variable , . This was something we could envision with two 2-dimensional plots (real and imaginary parts or magnitude andphase). However, with Z, we have a complex-valued function of a complex variable . In order to examine the magnitude and phase or real andimaginary parts of this function, we must examine 3-dimensional surface plots of each component.
Consider the z-transform given by , as illustrated below.

The corresponding DTFT has magnitude and phase given below.
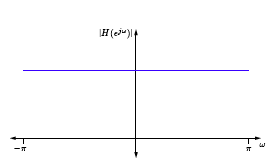

What could the system H be doing? It is a perfect all-pass, linear-phase system. But what does this mean?
Suppose . Then
Thus, is the -transform of a system that simply delays the input by . is the -transform of a unit-delay.
Now consider
What if ? Then does not converge! Therefore, whenever we compute a -tranform, we must also specify the set of 's for which the -transform exists. This is called the (ROC).
ztrans and
iztrans , that are both part of the
symbolic toolbox, and will find the Z and inverseZ transforms respectively. This method is generally
preferred for more complicated functions. Simpler and morecontrived functions are usually found easily enough by using
tables .The -transform might seem slightly ugly. We have to worry about the region of convergence, and stability issues, and so forth. However, in the end it is worthwhile because it proves extremely useful in analyzing digital filters with feedback. For example, consider the system illustrated below

We can analyze this system via the equations
and
More generally,
and
or equivalently,
What does the -transform of this relationship look like?
Note that
Thus the relationship reduces to
Hence, given a system the one above, we can easily determine the system's transfer function, and end up with a ratio of two polynomials in : a rational function. Similarly, given a rational function, it is easy to realize this function in a simple hardware architecture.
The z-transform proves a useful, more general form of the Discrete Time Fourier Transform. It applies equally well to describing systems as well as signals using the eigenfunction method, and proves extremely useful in digital filter design.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?