| << Chapter < Page | Chapter >> Page > |
This module contains review questions and answers keyed to the module titled GAME 2302-0120: Visualizing Column Matrices .
The questions and the answers are connected by hyperlinks to make it easy for you to navigate from the question to the answer and back again.
True or False: The following equation is the equation of a straight line in two dimensions where m is the slope, b is the y-intercept, and the asteriskindicates multiplication:
y = m*x + b
True or False: The following equation is the equation of a hyperbola in two dimensions where x^2 indicates x raised to the second power and k is they-intercept:
y = x^2 + k
In this and other questions that follow, the upper-case T represents transpose, as shown by a superscript T in the Kjell tutorial.
True or False: Given that a and b are column matrices, the following equations are true:
a = (3,2)T
b = (-2,1)T
a + b = (5,3)T
True or False: The addition of vectors depends on their location.
Consider Figure 1 .
Figure 1 Question 5
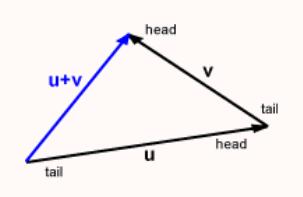
True or False: A valid statement of the head-to-tail rule is:
Head-to-Tail Rule: Move vector v (keeping its length and orientation the same) until its tail touches the tail of u. The sum is the vector from the tail of u to the head of v.
True or False: The head-to-tail rule works in both 2D and 3D.
True or False: The associative rule applies to the addition of vectors in alldimensions.
True or False: Vector addition is commutative, just like addition of real numbers.
True or False: The commutative rule for vectors applies in all dimensions.
True or False: A coordinate frame consists of a distinguished point P0 (called the origin) and an axis for each dimension (often called X and Y). In 2D space there are two axes; in 3D space there are three axes (often called X, Y, and Z).
True or False: Points can be represented with column matrices independently of the coordinate frame.
True or False: Because of the triangle inequality, the sum of two vectors is not necessarily the same as the sum of the lengths of the two vectors.
True or False: A displacement vector added to a point results in a point.
What is the meaning of the following two images?
These images were inserted here simply to insert some space between the questions and the answers to keep them from being visible on the screen at thesame time.
This image was also inserted for the purpose of inserting space between the questions and the answers.
True
Kjell, Chapter 3
True
Kjell, Chapter 3
False. The correct statement is:
Points can be represented with column matrices. To do this, you first need to decide on a coordinate frame (sometimes called just frame).
Kjell, Chapter 3
True
Kjell, Chapter 3
True
Kjell, Chapter 3
True
Kjell, Chapter 3
True
Kjell, Chapter 3
True
Kjell, Chapter 3
False. The correct statement is:
Head-to-Tail Rule: Move vector v (keeping its length and orientation the same) until its tail touches the head of u. The sum is the vector from the tail of u to the head of v.
Kjell, Chapter 3
False. Vectors have no position or location.
Kjell, Chapter 3.
False
a + b = (1,3)T
Kjell Chapter 3
False. This is the equation of a parabola, not a hyperbola.
True
This section contains a variety of miscellaneous information.
Financial : Although the Connexions site makes it possible for you to download aPDF file for this module at no charge, and also makes it possible for you to purchase a pre-printed version of the PDF file, youshould be aware that some of the HTML elements in this module may not translate well into PDF.
I also want you to know that, I receive no financial compensation from the Connexions website even if you purchase the PDF version ofthe module.
In the past, unknown individuals have copied my modules from cnx.org, converted them to Kindle books, and placed them for sale onAmazon.com showing me as the author. I neither receive compensation for those sales nor do I know who does receive compensation. If youpurchase such a book, please be aware that it is a copy of a module that is freely available on cnx.org and that it was made andpublished without my prior knowledge.
Affiliation : I am a professor of Computer Information Technology at Austin Community College in Austin, TX.
-end-

Notification Switch
Would you like to follow the 'Game 2302 - mathematical applications for game development' conversation and receive update notifications?