| << Chapter < Page | Chapter >> Page > |
How can the graph of be used to construct the graph of
Explain why the period of is equal to
Answers will vary. Using the unit circle, one can show that
Why are there no intercepts on the graph of
How does the period of compare with the period of
The period is the same:
For the following exercises, match each trigonometric function with one of the following graphs.

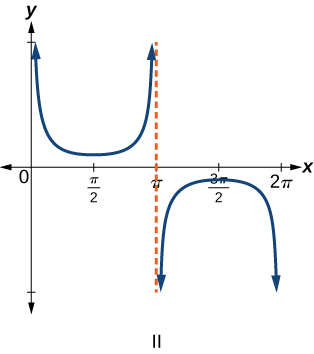
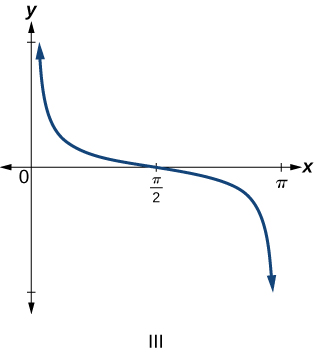
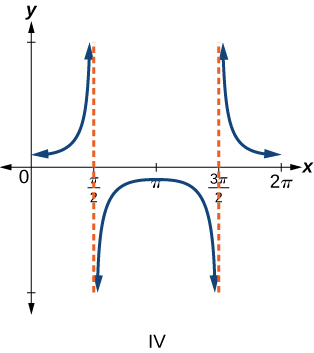
For the following exercises, find the period and horizontal shift of each of the functions.
For the following exercises, rewrite each expression such that the argument is positive.
For the following exercises, sketch two periods of the graph for each of the following functions. Identify the stretching factor, period, and asymptotes.
For the following exercises, find and graph two periods of the periodic function with the given stretching factor, period, and phase shift.
A tangent curve, period of and phase shift
For the following exercises, find an equation for the graph of each function.
For the following exercises, use a graphing calculator to graph two periods of the given function. Note: most graphing calculators do not have a cosecant button; therefore, you will need to input as
Graph What is the function shown in the graph?
The function marks the distance in the movement of a light beam from a police car across a wall for time in seconds, and distance in feet.
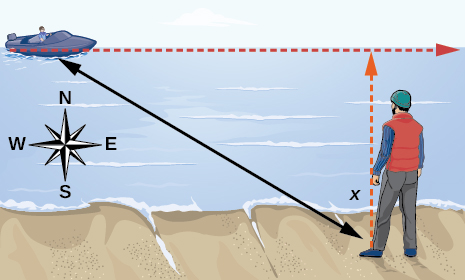
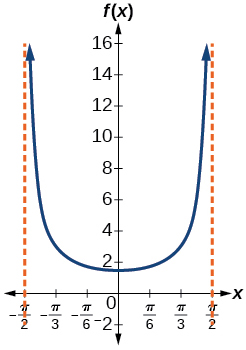
Standing on the shore of a lake, a fisherman sights a boat far in the distance to his left. Let measured in radians, be the angle formed by the line of sight to the ship and a line due north from his position. Assume due north is 0 and is measured negative to the left and positive to the right. (See [link] .) The boat travels from due west to due east and, ignoring the curvature of the Earth, the distance in kilometers, from the fisherman to the boat is given by the function
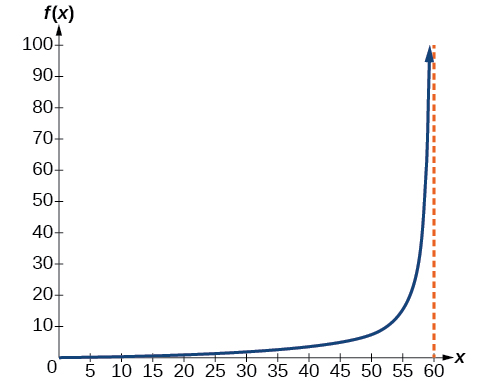
A laser rangefinder is locked on a comet approaching Earth. The distance in kilometers, of the comet after days, for in the interval 0 to 30 days, is given by
A video camera is focused on a rocket on a launching pad 2 miles from the camera. The angle of elevation from the ground to the rocket after seconds is

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?