| << Chapter < Page | Chapter >> Page > |
These approximations may be substituted into our original partial differential equation in order to solve for .
The second finite difference method used to solve the wave equation is the trapezoidal approximation method, where we have the system of equations
which we will denote as
where represents the identity matrix. The operator is a tridiagonal matrix with -2 along the diagonal and ones along the superdiagonal and subdiagonal. The approximating integral equation
is solved to reveal a solution for . The trapezoidal integration method turns out to be the more accurate of the two solution methods, since its error is less than the error of the forward Euler method. Real values for the string's tension, density, and length were used to evaluate the solution for the trapezoidal method, but gave us unintelligible results when used for the forward Euler method. Both methods were used to evaluate the solution using arbitrary values.
With all the preliminary work established, we can move on to the optimization problem. We investigated two objective functions for optimization. The first objective function considered was the following
Here a suitable time is preordained. It is legitimate to do this since damping should not affect the periodic details of the waveform. The is solved with the given and fitted to . We parameterize
which acts at one point on the string with a shape similar to the following.

It is important also that to guarantee the above shape. Our control problem then, is to
subject to solving our wave equation with the same initial and boundary conditions. There is a scaling issue since is small (on the order of ) at times. To correct this we scale our target so that the two waveforms are comparable before we run the optimization. Normalizing instead, would be cumbersome since the maximum amplitude depends on time. To expedite the optimizer, we supply the gradient of our objective
The equations for the partial derivatives are as follows.
The inner partial derivatives will be approximated by the same finite difference method we used above.
One of the main difficulties with this objective function is that it requires a to be found beforehand and thus we can only optimize with respect to our spacial dimension. Optimizing over both space and time would rid us of needing to find a good but complicates our objective function and retards our optimizer. Another concern with this objective is that it takes into account the sign of the target waveform, but whether the waveform is or is no matter to the musician. Along the same lines we have the scaling difficulty. Another objective function we have explored is the following energy minimization problem. We note that can be represented as a combination of sinusoids. For a given we have
Here each represents the nth Fourier coefficient that corresponds to the expression of the nth mode in the total wave. Since we are interested in expressing only the fourth mode, our optimization problem will try to minimize all other modes
subject to our wave equation with the same conditions. We decide on clearing up the first ten modes (except the fourth) to ensure that we are left with a waveform closest to our target. Like before we supply the gradient.
This objective function solves the sign and amplitude problems of the first. Additionally we are now optimizing over time so we need not specify a . One may wish to reset the bounds of the time integral through a different interval.
This is the result of our optimizer given a certain driving force using our first objective function.

This is the result of our optimizer at a certain time using the energy minimization objective. Since we optimized over space and time, we express this as a three dimensional plot.

For the energy minimization objective function using multiple dampings, we have this result.
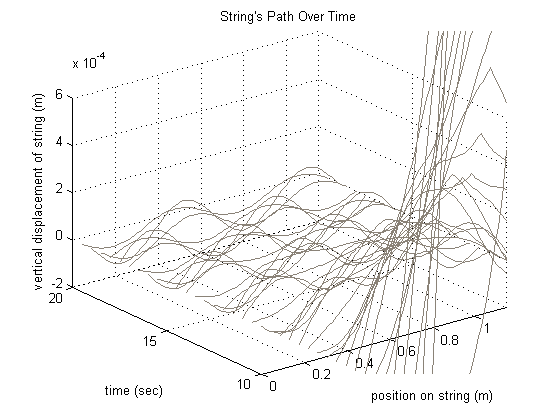
Comparatively, the values of the objective function for single and multiple dampings are on the same order of magnitude, with the value for the single dampings being slightly smaller. Therefore the optimization process for a single damping is more effective, but not by much.
We would like to give a big thanks to Dr. Steve Cox for his guidance and support throughout the course of the project. This paper describes work completed with the support of the NSF.
All of the codes used in this project are available on our website at
http://www.owlnet.rice.edu/ mlg6/strings/.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?