| << Chapter < Page | Chapter >> Page > |
We first detect edges using the Sobel operator [1], and then we apply the Hough circle transform to detect circles in the image [2.]The following steps we took will be covered in more detail under section 2.2.

Fig 2.1 From left to right: Original image, blurred image, image Edges, Hough transform results, processing the results of the Hough transform.
Software implementation was done with Python. The following Python libraries were used.
Blurring the image removes noise and filters out background details. To do this, we blur the image with a Gaussian kernel.
Fig 2.2 5x5 Gaussian kernel with a standard deviation of 1
Code
def blur(img, blursize):
""":param img: image to be blurred
:param blursize: size of gaussian kernel to blur with:return: blurred image
"""# =============================
# Generate Gaussian kernel# =============================
gauss = cv2.getGaussianKernel(blursize, blursize/3)gauss = np.outer(gauss, gauss)
# =============================# Filter with Gaussian kernel
# =============================img = cv2.filter2D(img, -1, gauss)
return img
Edges occur at large changes in pixel value, so by finding local maximums in the image gradient’s magnitude, we can detect edge points. This concept is illustrated in 1 dimension (1D) in Fig 2.3.
Fig 2.3 Edges occur at large changes in pixel value, or, local maximums in the derivative.
Convolving an image with the Sobel operator gives us the approximate partial derivatives in the x and y directions. Let us define The Sobel operator as Sx for the x direction and Sy for the y direction, let our define our image as A, and let us define Bx and By as the partial x and partial y, respectively, derivative approximations of A.
Fig 2.4 Sobel operators for approximating partial x and partial y derivatives
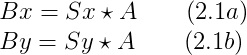
We can find the magnitude of gradient with equation 2.2, where the square and square root are element-wise operations.
![]()
Now let E be a boolean matrix of the same dimensions as the image where if a pixel is an edge, then the boolean value for the pixel is True. We calculate this matrix by determining a threshold tmag and declaring every pixel whose gradient magnitude is at least tmag an edge pixel
![]()
In our actual approach, we split the image into red, blue, and green channels. We perform edge detection on all 3 and recombine them with equation 2.4. This method allows us to find cleaner edges.
![]()
We can find the gradient of B with equation 2.5. Though it doesn’t factor into the method of edge detection used here, finding the gradient at edges is important for reducing computational complexity for the Hough transform.

Notification Switch
Would you like to follow the 'Hough transform object detection' conversation and receive update notifications?