| << Chapter < Page | Chapter >> Page > |
(b) When n = 5, there are five subshells of orbitals that we need to sum:
Again, each orbital holds two electrons, so 50 electrons can fit in this shell.
(c) The number of orbitals in any shell n will equal n 2 . There can be up to two electrons in each orbital, so the maximum number of electrons will be 2 n 2
n = 4
| Orbital | n | l | m l degeneracy | Radial nodes (no.) |
|---|---|---|---|---|
| 4 f | ||||
| 4 | 1 | |||
| 7 | 7 | 3 | ||
| 5 d |
| Orbital | n | l | m l degeneracy | Radial nodes (no.) |
|---|---|---|---|---|
| 4 f | 4 | 3 | 7 | 0 |
| 4 p | 4 | 1 | 3 | 2 |
| 7 f | 7 | 3 | 7 | 3 |
| 5 d | 5 | 2 | 5 | 2 |
The five degenerate 3 d orbitals
Macroscopic objects act as particles. Microscopic objects (such as electrons) have properties of both a particle and a wave. Their exact trajectories cannot be determined. The quantum mechanical model of atoms describes the three-dimensional position of the electron in a probabilistic manner according to a mathematical function called a wavefunction, often denoted as ψ . Atomic wavefunctions are also called orbitals. The squared magnitude of the wavefunction describes the distribution of the probability of finding the electron in a particular region in space. Therefore, atomic orbitals describe the areas in an atom where electrons are most likely to be found.
An atomic orbital is characterized by three quantum numbers. The principal quantum number, n , can be any positive integer. The general region for value of energy of the orbital and the average distance of an electron from the nucleus are related to n . Orbitals having the same value of n are said to be in the same shell. The angular momentum quantum number, l , can have any integer value from 0 to n – 1. This quantum number describes the shape or type of the orbital. Orbitals with the same principle quantum number and the same l value belong to the same subshell. The magnetic quantum number, m l , with 2 l + 1 values ranging from – l to + l , describes the orientation of the orbital in space. In addition, each electron has a spin quantum number, m s , that can be equal to No two electrons in the same atom can have the same set of values for all the four quantum numbers.
How are the Bohr model and the quantum mechanical model of the hydrogen atom similar? How are they different?
Both models have a central positively charged nucleus with electrons moving about the nucleus in accordance with the Coulomb electrostatic potential. The Bohr model assumes that the electrons move in circular orbits that have quantized energies, angular momentum, and radii that are specified by a single quantum number, n = 1, 2, 3, …, but this quantization is an ad hoc assumption made by Bohr to incorporate quantization into an essentially classical mechanics description of the atom. Bohr also assumed that electrons orbiting the nucleus normally do not emit or absorb electromagnetic radiation, but do so when the electron switches to a different orbit. In the quantum mechanical model, the electrons do not move in precise orbits (such orbits violate the Heisenberg uncertainty principle) and, instead, a probabilistic interpretation of the electron’s position at any given instant is used, with a mathematical function ψ called a wavefunction that can be used to determine the electron’s spatial probability distribution. These wavefunctions, or orbitals, are three-dimensional stationary waves that can be specified by three quantum numbers that arise naturally from their underlying mathematics (no ad hoc assumptions required): the principal quantum number, n (the same one used by Bohr), which specifies shells such that orbitals having the same n all have the same energy and approximately the same spatial extent; the angular momentum quantum number l , which is a measure of the orbital’s angular momentum and corresponds to the orbitals’ general shapes, as well as specifying subshells such that orbitals having the same l (and n ) all have the same energy; and the orientation quantum number m , which is a measure of the z component of the angular momentum and corresponds to the orientations of the orbitals. The Bohr model gives the same expression for the energy as the quantum mechanical expression and, hence, both properly account for hydrogen’s discrete spectrum (an example of getting the right answers for the wrong reasons, something that many chemistry students can sympathize with), but gives the wrong expression for the angular momentum (Bohr orbits necessarily all have non-zero angular momentum, but some quantum orbitals [ s orbitals] can have zero angular momentum).
What are the allowed values for each of the four quantum numbers: n , l , m l , and m s ?
Describe the properties of an electron associated with each of the following four quantum numbers: n , l , m l , and m s .
n determines the general range for the value of energy and the probable distances that the electron can be from the nucleus. l determines the shape of the orbital. m 1 determines the orientation of the orbitals of the same l value with respect to one another. m s determines the spin of an electron.
Answer the following questions:
(a) Without using quantum numbers, describe the differences between the shells, subshells, and orbitals of an atom.
(b) How do the quantum numbers of the shells, subshells, and orbitals of an atom differ?
Identify the subshell in which electrons with the following quantum numbers are found:
(a) n = 2, l = 1
(b) n = 4, l = 2
(c) n = 6, l = 0
(a) 2 p ; (b) 4 d ; (c) 6 s
Which of the subshells described in the previous question contain degenerate orbitals? How many degenerate orbitals are in each?
Identify the subshell in which electrons with the following quantum numbers are found:
(a) n = 3, l = 2
(b) n = 1, l = 0
(c) n = 4, l = 3
(a) 3 d; (b) 1 s; (c) 4 f
Which of the subshells described in the previous question contain degenerate orbitals? How many degenerate orbitals are in each?
Sketch the boundary surface of a and a p y orbital. Be sure to show and label the axes.
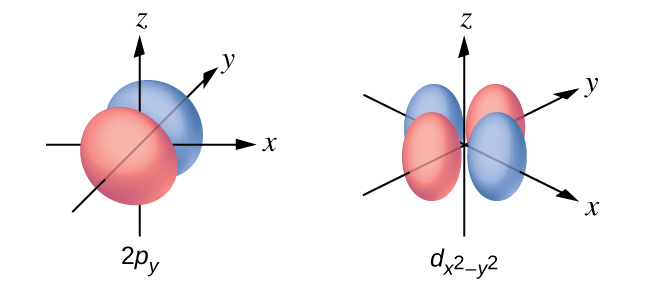
Sketch the p x and d xz orbitals. Be sure to show and label the coordinates.
Consider the orbitals shown here in outline.
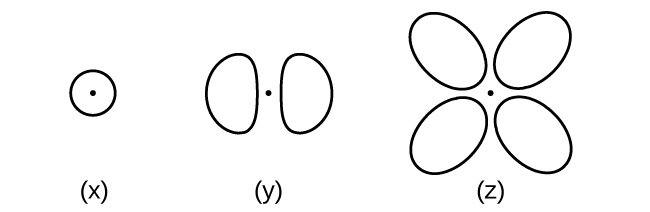
(a) What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?
(b) How many orbitals of type (x) are found in a shell with n = 2? How many of type (y)? How many of type (z)?
(c) Write a set of quantum numbers for an electron in an orbital of type (x) in a shell with n = 4. Of an orbital of type (y) in a shell with n = 2. Of an orbital of type (z) in a shell with n = 3.
(d) What is the smallest possible n value for an orbital of type (x)? Of type (y)? Of type (z)?
(e) What are the possible l and m l values for an orbital of type (x)? Of type (y)? Of type (z)?
(a) x. 2, y. 2, z. 2; (b) x. 1, y. 3, z. 0; (c) x. 4 0 0 y. 2 1 0 z. 3 2 0 (d) x. 1, y. 2, z. 3; (e) x. l = 0, m l = 0, y. l = 1, m l = –1, 0, or + 1, z. l = 2, m l = –2, –1, 0, +1, +2
State the Heisenberg uncertainty principle. Describe briefly what the principle implies.
How many electrons could be held in the second shell of an atom if the spin quantum number m s could have three values instead of just two? (Hint: Consider the Pauli exclusion principle.)
12
Which of the following equations describe particle-like behavior? Which describe wavelike behavior? Do any involve both types of behavior? Describe the reasons for your choices.
(a) c = λν
(b)
(c)
(d) E = hν
(e)
Write a set of quantum numbers for each of the electrons with an n of 4 in a Se atom.
| n | l | m l | s |
|---|---|---|---|
| 4 | 0 | 0 | |
| 4 | 0 | 0 | |
| 4 | 1 | −1 | |
| 4 | 1 | 0 | |
| 4 | 1 | +1 | |
| 4 | 1 | −1 |

Notification Switch
Would you like to follow the 'Chemistry' conversation and receive update notifications?