| << Chapter < Page | Chapter >> Page > |
The values n f and n i are the final and initial energy states of the electron. [link] in the previous section of the chapter demonstrates calculations of such energy changes.
The principal quantum number is one of three quantum numbers used to characterize an orbital. An atomic orbital , which is distinct from an orbit , is a general region in an atom within which an electron is most probable to reside. The quantum mechanical model specifies the probability of finding an electron in the three-dimensional space around the nucleus and is based on solutions of the Schrödinger equation. In addition, the principle quantum number defines the energy of an electron in a hydrogen or hydrogen-like atom or an ion (an atom or an ion with only one electron) and the general region in which discrete energy levels of electrons in a multi-electron atoms and ions are located.
Another quantum number is l , the angular momentum quantum number . It is an integer that defines the shape of the orbital, and takes on the values, l = 0, 1, 2, …, n – 1. This means that an orbital with n = 1 can have only one value of l , l = 0, whereas n = 2 permits l = 0 and l = 1, and so on. The principal quantum number defines the general size and energy of the orbital. The l value specifies the shape of the orbital. Orbitals with the same value of l form a subshell . In addition, the greater the angular momentum quantum number, the greater is the angular momentum of an electron at this orbital.
Orbitals with l = 0 are called s orbitals (or the s subshells). The value l = 1 corresponds to the p orbitals. For a given n , p orbitals constitute a p subshell (e.g., 3 p if n = 3). The orbitals with l = 2 are called the d orbitals , followed by the f-, g-, and h- orbitals for l = 3, 4, 5, and there are higher values we will not consider.
There are certain distances from the nucleus at which the probability density of finding an electron located at a particular orbital is zero. In other words, the value of the wavefunction ψ is zero at this distance for this orbital. Such a value of radius r is called a radial node. The number of radial nodes in an orbital is n – l – 1.
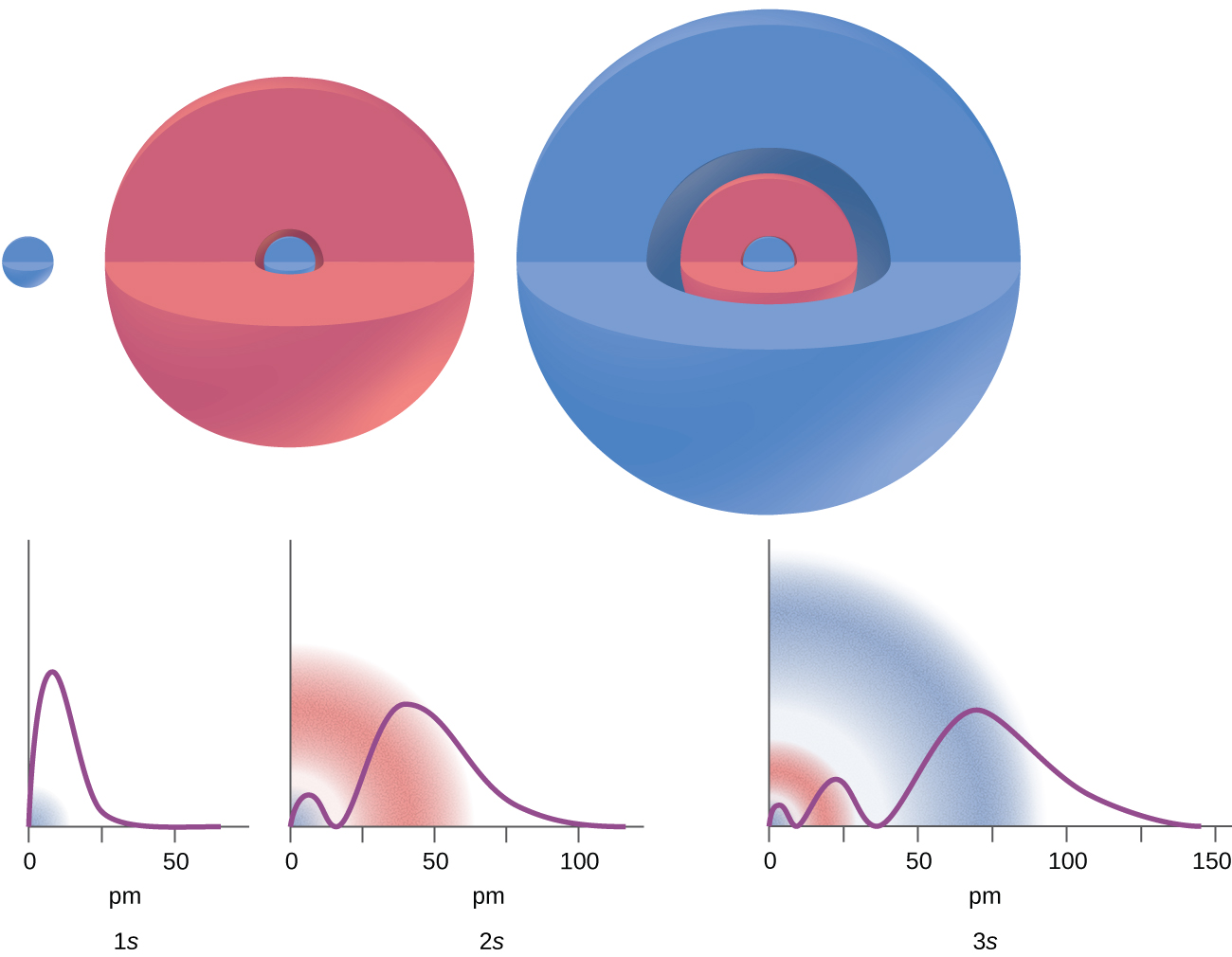
Consider the examples in [link] . The orbitals depicted are of the s type, thus l = 0 for all of them. It can be seen from the graphs of the probability densities that there are 1 – 0 – 1 = 0 places where the density is zero (nodes) for 1 s ( n = 1), 2 – 0 – 1 = 1 node for 2 s , and 3 – 0 – 1 = 2 nodes for the 3 s orbitals.
The s subshell electron density distribution is spherical and the p subshell has a dumbbell shape. The d and f orbitals are more complex. These shapes represent the three-dimensional regions within which the electron is likely to be found.
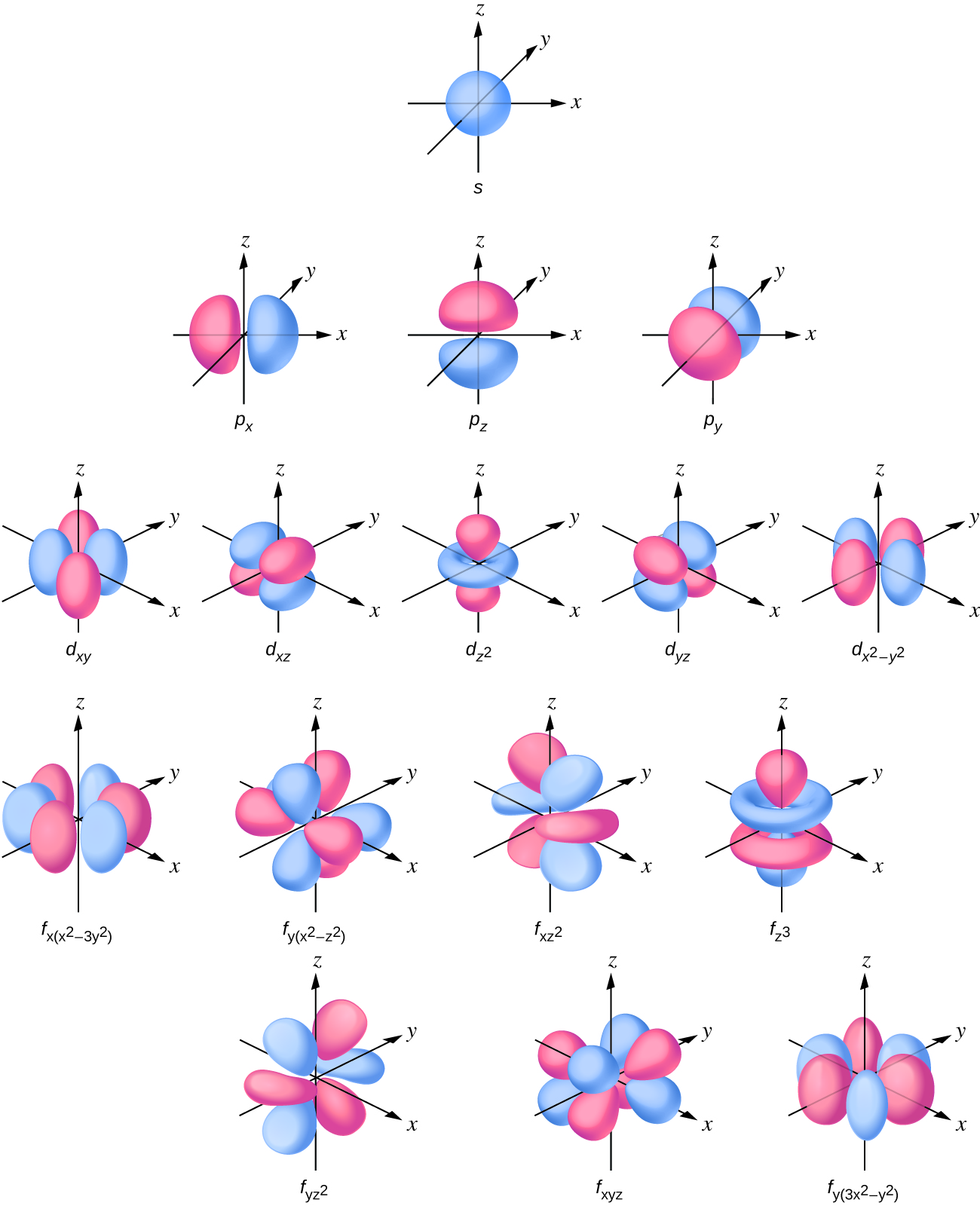
If an electron has an angular momentum ( l ≠ 0), then this vector can point in different directions. In addition, the z component of the angular momentum can have more than one value. This means that if a magnetic field is applied in the z direction, orbitals with different values of the z component of the angular momentum will have different energies resulting from interacting with the field. The magnetic quantum number , called m l, specifies the z component of the angular momentum for a particular orbital. For example, for an s orbital, l = 0, and the only value of m l is zero. For p orbitals, l = 1, and m l can be equal to –1, 0, or +1. Generally speaking, m l can be equal to – l , –( l – 1), …, –1, 0, +1, …, ( l – 1), l . The total number of possible orbitals with the same value of l (a subshell) is 2 l + 1. Thus, there is one s -orbital for ml = 0 , there are three p -orbitals for ml = 1 , five d -orbitals for ml = 2 , seven f -orbitals for ml = 3 , and so forth. The principle quantum number defines the general value of the electronic energy. The angular momentum quantum number determines the shape of the orbital. And the magnetic quantum number specifies orientation of the orbital in space, as can be seen in [link] .

Notification Switch
Would you like to follow the 'Chemistry' conversation and receive update notifications?