| << Chapter < Page | Chapter >> Page > |
Consider the region depicted in the following figure. Find the area of
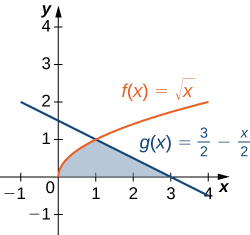
units 2
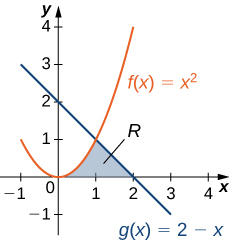
In [link] , we had to evaluate two separate integrals to calculate the area of the region. However, there is another approach that requires only one integral. What if we treat the curves as functions of instead of as functions of Review [link] . Note that the left graph, shown in red, is represented by the function We could just as easily solve this for and represent the curve by the function (Note that is also a valid representation of the function as a function of However, based on the graph, it is clear we are interested in the positive square root.) Similarly, the right graph is represented by the function but could just as easily be represented by the function When the graphs are represented as functions of we see the region is bounded on the left by the graph of one function and on the right by the graph of the other function. Therefore, if we integrate with respect to we need to evaluate one integral only. Let’s develop a formula for this type of integration.
Let and be continuous functions over an interval such that for all We want to find the area between the graphs of the functions, as shown in the following figure.
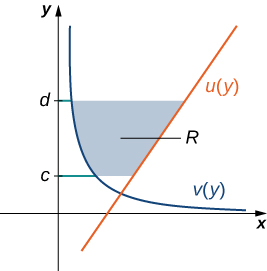
This time, we are going to partition the interval on the and use horizontal rectangles to approximate the area between the functions. So, for let be a regular partition of Then, for choose a point then over each interval construct a rectangle that extends horizontally from to [link] (a) shows the rectangles when is selected to be the lower endpoint of the interval and [link] (b) shows a representative rectangle in detail.

The height of each individual rectangle is and the width of each rectangle is Therefore, the area between the curves is approximately
This is a Riemann sum, so we take the limit as obtaining
These findings are summarized in the following theorem.
Let and be continuous functions such that for all Let denote the region bounded on the right by the graph of on the left by the graph of and above and below by the lines and respectively. Then, the area of is given by
Let’s revisit [link] , only this time let’s integrate with respect to Let be the region depicted in [link] . Find the area of by integrating with respect to
We must first express the graphs as functions of As we saw at the beginning of this section, the curve on the left can be represented by the function and the curve on the right can be represented by the function
Now we have to determine the limits of integration. The region is bounded below by the x -axis, so the lower limit of integration is The upper limit of integration is determined by the point where the two graphs intersect, which is the point so the upper limit of integration is Thus, we have
Calculating the area of the region, we get
The area of the region is units 2 .

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?