4.5 Derivatives and the shape of a graph (Page 6/14)

Calculus volume 1 Page 6 / 14

Consider the function $f (x) = x^{3} - (\frac{3}{2}) x^{2} - 18 x .$ The points $c = 3, −2$ satisfy $f^{'} (c) = 0 .$ Use the second derivative test to determine whether $f$ has a local maximum or local minimum at those points.

$f$ has a local maximum at $−2$ and a local minimum at $3 .$

Got questions? Get instant answers now!

We have now developed the tools we need to determine where a function is increasing and decreasing, as well as acquired an understanding of the basic shape of the graph. In the next section we discuss what happens to a function as $x \to ± \infty .$ At that point, we have enough tools to provide accurate graphs of a large variety of functions.

Key concepts

If $c$ is a critical point of $f$ and $f^{'} (x) > 0$ for $x < c$ and $f^{'} (x) < 0$ for $x > c,$ then $f$ has a local maximum at $c .$
If $c$ is a critical point of $f$ and $f^{'} (x) < 0$ for $x < c$ and $f^{'} (x) > 0$ for $x > c,$ then $f$ has a local minimum at $c .$
If $f ″ (x) > 0$ over an interval $I,$ then $f$ is concave up over $I .$
If $f ″ (x) < 0$ over an interval $I,$ then $f$ is concave down over $I .$
If $f^{'} (c) = 0$ and $f ″ (c) > 0,$ then $f$ has a local minimum at $c .$
If $f^{'} (c) = 0$ and $f ″ (c) < 0,$ then $f$ has a local maximum at $c .$
If $f^{'} (c) = 0$ and $f ″ (c) = 0,$ then evaluate $f^{'} (x)$ at a test point $x$ to the left of $c$ and a test point $x$ to the right of $c,$ to determine whether $f$ has a local extremum at $c .$

If $c$ is a critical point of $f (x),$ when is there no local maximum or minimum at $c ?$ Explain.

Got questions? Get instant answers now!

For the function $y = x^{3},$ is $x = 0$ both an inflection point and a local maximum/minimum?

It is not a local maximum/minimum because $f^{'}$ does not change sign

Got questions? Get instant answers now!

For the function $y = x^{3},$ is $x = 0$ an inflection point?

Got questions? Get instant answers now!

Is it possible for a point $c$ to be both an inflection point and a local extrema of a twice differentiable function?

Got questions? Get instant answers now!

Why do you need continuity for the first derivative test? Come up with an example.

Got questions? Get instant answers now!

Explain whether a concave-down function has to cross $y = 0$ for some value of $x .$

False; for example, $y = \sqrt{x} .$

Got questions? Get instant answers now!

Explain whether a polynomial of degree $2$ can have an inflection point.

Got questions? Get instant answers now!

For the following exercises, analyze the graphs of $f^{'},$ then list all intervals where $f$ is increasing or decreasing.

The function f’(x) is graphed. The function starts negative and crosses the x axis at (−2, 0). Then it continues increasing a little before decreasing and crossing the x axis at (−1, 0). It achieves a local minimum at (1, −6) before increasing and crossing the x axis at (2, 0).

Increasing for $−2 < x < −1$ and $x > 2;$ decreasing for $x < −2$ and $−1 < x < 2$

Got questions? Get instant answers now!

The function f’(x) is graphed. The function starts negative and touches the x axis at the origin. Then it decreases a little before increasing to cross the x axis at (1, 0) and continuing to increase.

Decreasing for $x < 1,$ increasing for $x > 1$

Got questions? Get instant answers now!

The function f’(x) is graphed. The function starts positive and decreases to touch the x axis at (−1, 0). Then it increases to (0, 4.5) before decreasing to touch the x axis at (1, 0). Then the function increases.

Got questions? Get instant answers now!

The function f’(x) is graphed. The function starts at (−2, 0), decreases to (−1.5, −1.5), increases to (−1, 0), and continues increasing before decreasing to the origin. Then the other side is symmetric: that is, the function increases and then decreases to pass through (1, 0). It continues decreasing to (1.5, −1.5), and then increase to (2, 0).

Decreasing for $−2 < x < −1$ and $1 < x < 2;$ increasing for $−1 < x < 1$ and $x < −2$ and $x > 2$

Got questions? Get instant answers now!

For the following exercises, analyze the graphs of $f^{'},$ then list all intervals where

$f$ is increasing and decreasing and
the minima and maxima are located.

The function f’(x) is graphed. The function starts at (−2, 0), decreases for a little and then increases to (−1, 0), continues increasing before decreasing to the origin, at which point it increases.

Got questions? Get instant answers now!

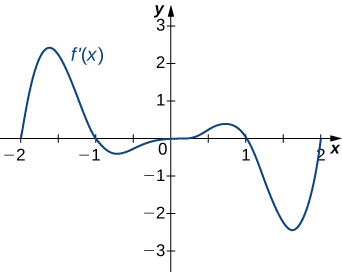
The function f’(x) is graphed. The function starts at (−2, 0), increases and then decreases to (−1, 0), decreases and then increases to an inflection point at the origin. Then the function increases and decreases to cross (1, 0). It continues decreasing and then increases to (2, 0).

a. Increasing over $−2 < x < −1, 0 < x < 1, x > 2,$ decreasing over $x < −2,$ $−1 < x < 0, 1 < x < 2;$ b. maxima at $x = −1$ and $x = 1,$ minima at $x = −2$ and $x = 0$ and $x = 2$

Got questions? Get instant answers now!

The function f’(x) is graphed from x = −2 to x = 2. It starts near zero at x = −2, but then increases rapidly and remains positive for the entire length of the graph.

Got questions? Get instant answers now!

The function f’(x) is graphed. The function starts negative and crosses the x axis at the origin, which is an inflection point. Then it continues increasing.

a. Increasing over $x > 0,$ decreasing over $x < 0;$ b. Minimum at $x = 0$

Got questions? Get instant answers now!

The function f’(x) is graphed. The function starts negative and crosses the x axis at (−1, 0). Then it continues increasing a little before decreasing and touching the x axis at the origin. It increases again and then decreases to (1, 0). Then it increases.

Got questions? Get instant answers now!

For the following exercises, analyze the graphs of $f^{'},$ then list all inflection points and intervals $f$ that are concave up and concave down.

The function f’(x) is graphed. The function is linear and starts negative. It crosses the x axis at the origin.

Concave up on all $x,$ no inflection points

Got questions? Get instant answers now!

The function f’(x) is graphed. It is an upward-facing parabola with 0 as its local minimum.

Got questions? Get instant answers now!

The function f’(x) is graphed. The function resembles the graph of x3: that is, it starts negative and crosses the x axis at the origin. Then it continues increasing.

Concave up on all $x,$ no inflection points

Got questions? Get instant answers now!

The function f’(x) is graphed. The function starts negative and crosses the x axis at (−0.5, 0). Then it continues increasing to (0, 1.5) before decreasing and touching the x axis at (1, 0). It then increases.

Got questions? Get instant answers now!

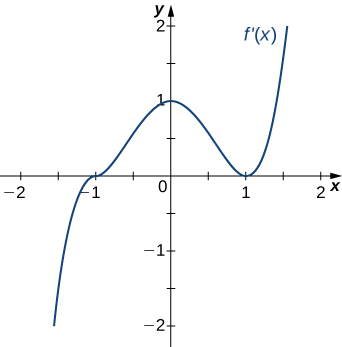
The function f’(x) is graphed. The function starts negative and crosses the x axis at (−1, 0). Then it continues increasing to a local maximum at (0, 1), at which point it decreases and touches the x axis at (1, 0). It then increases.

Concave up for $x < 0$ and $x > 1,$ concave down for $0 < x < 1,$ inflection points at $x = 0$ and $x = 1$

Got questions? Get instant answers now!

For the following exercises, draw a graph that satisfies the given specifications for the domain $x = [−3, 3] .$ The function does not have to be continuous or differentiable.

$f (x) > 0, f^{'} (x) > 0$ over $x > 1, −3 < x < 0, f^{'} (x) = 0$ over $0 < x < 1$

Got questions? Get instant answers now!

$f^{'} (x) > 0$ over $x > 2, −3 < x < −1, f^{'} (x) < 0$ over $−1 < x < 2, f ″ (x) < 0$ for all $x$

Answers will vary

Got questions? Get instant answers now!

$f ″ (x) < 0$ over $−1 < x < 1, f ″ (x) > 0, −3 < x < −1, 1 < x < 3,$ local maximum at $x = 0,$ local minima at $x = ± 2$

Got questions? Get instant answers now!

There is a local maximum at $x = 2,$ local minimum at $x = 1,$ and the graph is neither concave up nor concave down.

Answers will vary

Got questions? Get instant answers now!

Questions & Answers

prostaglandin and fever

Maha Reply

Discuss the differences between taste and flavor, including how other sensory inputs contribute to our perception of flavor.

John Reply

taste refers to your understanding of the flavor . while flavor one The other hand is refers to sort of just a blend things.

Faith

While taste primarily relies on our taste buds, flavor involves a complex interplay between taste and aroma

Kamara

which drugs can we use for ulcers

Ummi Reply

omeprazole

Kamara

what

Renee

what is this

Renee

is a drug

Kamara

of anti-ulcer

Kamara

Omeprazole Cimetidine / Tagament For the complicated once ulcer - kit

Patrick

what is the function of lymphatic system

Nency Reply

Not really sure

Eli

to drain extracellular fluid all over the body.

asegid

The lymphatic system plays several crucial roles in the human body, functioning as a key component of the immune system and contributing to the maintenance of fluid balance. Its main functions include: 1. Immune Response: The lymphatic system produces and transports lymphocytes, which are a type of

asegid

to transport fluids fats proteins and lymphocytes to the blood stream as lymph

Adama

what is anatomy

Oyindarmola Reply

Anatomy is the identification and description of the structures of living things

Kamara

what's the difference between anatomy and physiology

Oyerinde Reply

Anatomy is the study of the structure of the body, while physiology is the study of the function of the body. Anatomy looks at the body's organs and systems, while physiology looks at how those organs and systems work together to keep the body functioning.

AI-Robot

what is enzymes all about?

Mohammed Reply

Enzymes are proteins that help speed up chemical reactions in our bodies. Enzymes are essential for digestion, liver function and much more. Too much or too little of a certain enzyme can cause health problems

Kamara

yes

Prince

how does the stomach protect itself from the damaging effects of HCl

Wulku Reply

little girl okay how does the stomach protect itself from the damaging effect of HCL

Wulku

it is because of the enzyme that the stomach produce that help the stomach from the damaging effect of HCL

Kamara

function of digestive system

Ali Reply

function of digestive

Ali

the diagram of the lungs

Adaeze Reply

what is the normal body temperature

Diya Reply

37 degrees selcius

Xolo

37°c

Stephanie

please why 37 degree selcius normal temperature

Mark

36.5

Simon

37°c

Iyogho

the normal temperature is 37°c or 98.6 °Fahrenheit is important for maintaining the homeostasis in the body the body regular this temperature through the process called thermoregulation which involves brain skin muscle and other organ working together to maintain stable internal temperature

Stephanie

37A c

Wulku

what is anaemia

Diya Reply

anaemia is the decrease in RBC count hemoglobin count and PVC count

Eniola

what is the pH of the vagina

Diya Reply

how does Lysin attack pathogens

Diya

acid

Mary

I information on anatomy position and digestive system and there enzyme

Elisha Reply

anatomy of the female external genitalia

Muhammad Reply

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 1. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11964/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?

Ask

©flickr: Abraham	Multicellular Organisms Test By Monty Hartfield Start Test
	2 Psychology MCQ 2009 1 Exam By John Gabrieli Start Exam
©flickr: Abraham	3 Biology 3 By Sarah Warren Start Test
	Power Enigeering types of bearing lubrication By Sam Luong Start Quiz
	Professional makeup certification Test By Angela January Start Quiz
	12 AP 12 Nervous Tissue MCQ By OpenStax Start Quiz
	Managerial Psychology Exam By Dan Ariely Start Exam
	Capitalism Market Economy By Robert Murphy Start Test
	5 Lec:5 Case-control Studies By Janet Forrester Start Quiz
	Social Work midterm By Katy Pratt Start Exam