| << Chapter < Page | Chapter >> Page > |
Evaluate each of the following indefinite integrals:
We look at techniques for integrating a large variety of functions involving products, quotients, and compositions later in the text. Here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations.
A differential equation is an equation that relates an unknown function and one or more of its derivatives. The equation
is a simple example of a differential equation. Solving this equation means finding a function with a derivative Therefore, the solutions of [link] are the antiderivatives of If is one antiderivative of every function of the form is a solution of that differential equation. For example, the solutions of
are given by
Sometimes we are interested in determining whether a particular solution curve passes through a certain point —that is, The problem of finding a function that satisfies a differential equation
with the additional condition
is an example of an initial-value problem . The condition is known as an initial condition . For example, looking for a function that satisfies the differential equation
and the initial condition
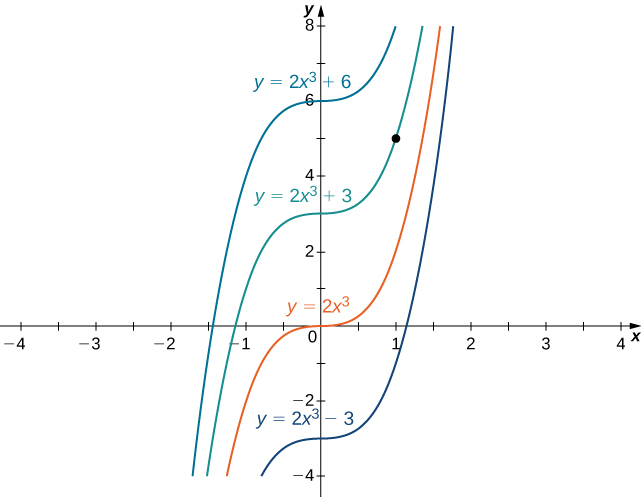
is an example of an initial-value problem. Since the solutions of the differential equation are to find a function that also satisfies the initial condition, we need to find such that From this equation, we see that and we conclude that is the solution of this initial-value problem as shown in the following graph.
Solve the initial-value problem
First we need to solve the differential equation. If then
Next we need to look for a solution that satisfies the initial condition. The initial condition means we need a constant such that Therefore,
The solution of the initial-value problem is

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?