| << Chapter < Page | Chapter >> Page > |
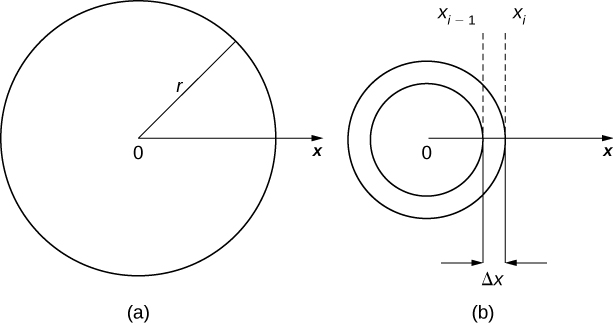
We now approximate the density and area of the washer to calculate an approximate mass, Note that the area of the washer is given by
You may recall that we had an expression similar to this when we were computing volumes by shells. As we did there, we use to approximate the average radius of the washer. We obtain
Using to approximate the density of the washer, we approximate the mass of the washer by
Adding up the masses of the washers, we see the mass of the entire disk is approximated by
We again recognize this as a Riemann sum, and take the limit as This gives us
We summarize these findings in the following theorem.
Let be an integrable function representing the radial density of a disk of radius Then the mass of the disk is given by
Let represent the radial density of a disk. Calculate the mass of a disk of radius 4.
Applying the formula, we find
Let represent the radial density of a disk. Calculate the mass of a disk of radius 2.
We now consider work. In physics, work is related to force, which is often intuitively defined as a push or pull on an object. When a force moves an object, we say the force does work on the object. In other words, work can be thought of as the amount of energy it takes to move an object. According to physics, when we have a constant force, work can be expressed as the product of force and distance.
In the English system, the unit of force is the pound and the unit of distance is the foot, so work is given in foot-pounds. In the metric system, kilograms and meters are used. One newton is the force needed to accelerate kilogram of mass at the rate of m/sec 2 . Thus, the most common unit of work is the newton-meter. This same unit is also called the joule . Both are defined as kilograms times meters squared over seconds squared
When we have a constant force, things are pretty easy. It is rare, however, for a force to be constant. The work done to compress (or elongate) a spring, for example, varies depending on how far the spring has already been compressed (or stretched). We look at springs in more detail later in this section.
Suppose we have a variable force that moves an object in a positive direction along the x -axis from point to point To calculate the work done, we partition the interval and estimate the work done over each subinterval. So, for let be a regular partition of the interval and for choose an arbitrary point To calculate the work done to move an object from point to point we assume the force is roughly constant over the interval, and use to approximate the force. The work done over the interval then, is given by

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?