| << Chapter < Page | Chapter >> Page > |
Suppose three point masses are placed on a number line as follows (assume coordinates are given in meters):
Find the center of mass of the system.
m
So far we have looked at systems of point masses on a line and in a plane. Now, instead of having the mass of a system concentrated at discrete points, we want to look at systems in which the mass of the system is distributed continuously across a thin sheet of material. For our purposes, we assume the sheet is thin enough that it can be treated as if it is two-dimensional. Such a sheet is called a lamina . Next we develop techniques to find the center of mass of a lamina. In this section, we also assume the density of the lamina is constant.
Laminas are often represented by a two-dimensional region in a plane. The geometric center of such a region is called its centroid . Since we have assumed the density of the lamina is constant, the center of mass of the lamina depends only on the shape of the corresponding region in the plane; it does not depend on the density. In this case, the center of mass of the lamina corresponds to the centroid of the delineated region in the plane. As with systems of point masses, we need to find the total mass of the lamina, as well as the moments of the lamina with respect to the x - and y -axes.
We first consider a lamina in the shape of a rectangle. Recall that the center of mass of a lamina is the point where the lamina balances. For a rectangle, that point is both the horizontal and vertical center of the rectangle. Based on this understanding, it is clear that the center of mass of a rectangular lamina is the point where the diagonals intersect, which is a result of the symmetry principle , and it is stated here without proof.
If a region R is symmetric about a line l , then the centroid of R lies on l .
Let’s turn to more general laminas. Suppose we have a lamina bounded above by the graph of a continuous function below by the x -axis, and on the left and right by the lines and respectively, as shown in the following figure.
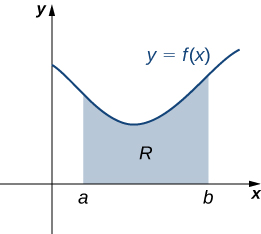
As with systems of point masses, to find the center of mass of the lamina, we need to find the total mass of the lamina, as well as the moments of the lamina with respect to the x - and y -axes. As we have done many times before, we approximate these quantities by partitioning the interval and constructing rectangles.
For let be a regular partition of Recall that we can choose any point within the interval as our In this case, we want to be the x -coordinate of the centroid of our rectangles. Thus, for we select such that is the midpoint of the interval. That is, Now, for construct a rectangle of height on The center of mass of this rectangle is as shown in the following figure.
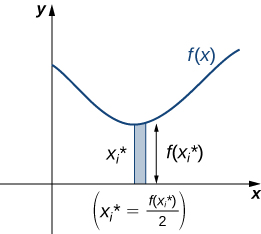

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?