6.2 Determining volumes by slicing  (Page 4/12)

Let’s look at some examples.

Using the disk method to find the volume of a solid of revolution 1

Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of $f\left(x\right)=\sqrt{x}$ and the $x\text{-axis}$ over the interval $\left[1,4\right]$ around the $x\text{-axis}\text{.}$

The graphs of the function and the solid of revolution are shown in the following figure.

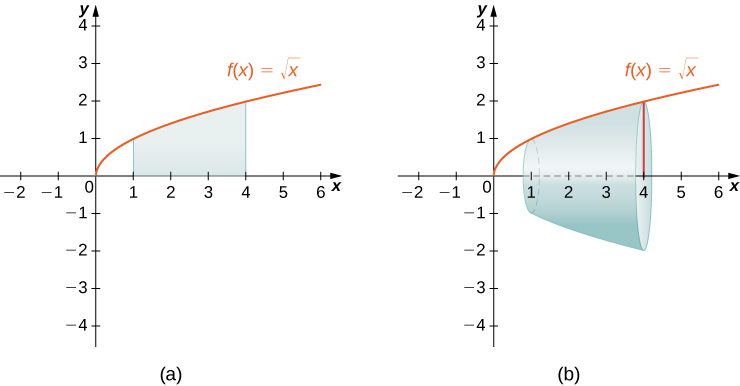
We have

$\begin{array}{cc}\hfill V& ={\displaystyle {\int }_a^b\pi {\left[f\left(x\right)\right]}^{2}dx}\hfill \\ & ={\displaystyle {\int }_1^4\pi {\left[\sqrt{x}\right]}^2}dx=\pi {\displaystyle {\int }_1^{4}xdx}\hfill \\ & ={\frac{\pi }{2}{x}^2|}_1^4=\frac{15\pi }{2}.\hfill \end{array}$

The volume is $\left(15\pi \right)\text{/}2$ units ³ .

Got questions? Get instant answers now!

Got questions? Get instant answers now!

So far, our examples have all concerned regions revolved around the $x\text{-axis,}$ but we can generate a solid of revolution by revolving a plane region around any horizontal or vertical line. In the next example, we look at a solid of revolution that has been generated by revolving a region around the $y\text{-axis}\text{.}$ The mechanics of the disk method are nearly the same as when the $x\text{-axis}$ is the axis of revolution, but we express the function in terms of $y$ and we integrate with respect to y as well. This is summarized in the following rule.

The next example shows how this rule works in practice.

Using the disk method to find the volume of a solid of revolution 2

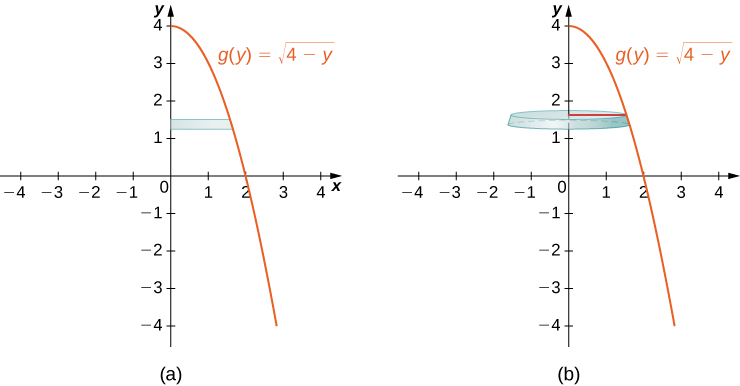
Let $R$ be the region bounded by the graph of $g\left(y\right)=\sqrt{4-y}$ and the $y\text{-axis}$ over the $y\text{-axis}$ interval $\left[0,4\right].$ Use the disk method to find the volume of the solid of revolution generated by rotating $R$ around the $y\text{-axis}\text{.}$

[link] shows the function and a representative disk that can be used to estimate the volume. Notice that since we are revolving the function around the $y\text{-axis,}$ the disks are horizontal, rather than vertical.

The region to be revolved and the full solid of revolution are depicted in the following figure.

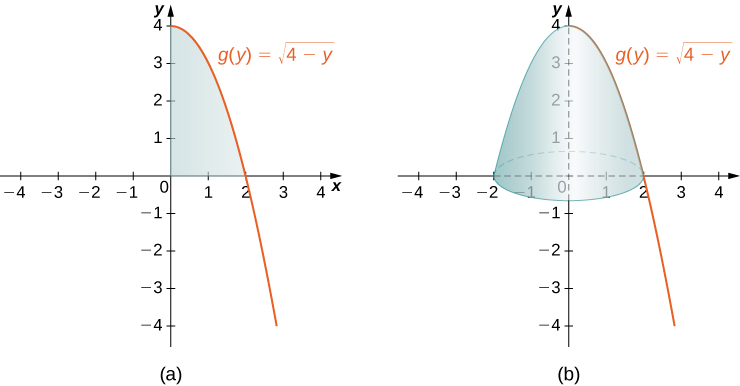
To find the volume, we integrate with respect to $y.$ We obtain

$\begin{array}{cc}\hfill V& ={\displaystyle {\int }_c^d\pi }{\left[g\left(y\right)\right]}^{2}dy\hfill \\ & ={\displaystyle {\int }_0^4\pi }{\left[\sqrt{4-y}\right]}^{2}dy=\pi {\displaystyle {\int }_0^4\left(4-y\right)}dy\hfill \\ & ={\pi \left[4y-\frac{y^2}{2}\right]|}_0^4=8\pi .\hfill \end{array}$

The volume is $8\pi$ units ³ .

Got questions? Get instant answers now!

Got questions? Get instant answers now!