| << Chapter < Page | Chapter >> Page > |
In business, companies are interested in maximizing revenue . In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.
Owners of a car rental company have determined that if they charge customers dollars per day to rent a car, where the number of cars they rent per day can be modeled by the linear function If they charge per day or less, they will rent all their cars. If they charge per day or more, they will not rent any cars. Assuming the owners plan to charge customers between $50 per day and per day to rent a car, how much should they charge to maximize their revenue?
Step 1: Let be the price charged per car per day and let be the number of cars rented per day. Let be the revenue per day.
Step 2: The problem is to maximize
Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is,
Step 4: Since the number of cars rented per day is modeled by the linear function the revenue can be represented by the function
Step 5: Since the owners plan to charge between per car per day and per car per day, the problem is to find the maximum revenue for in the closed interval
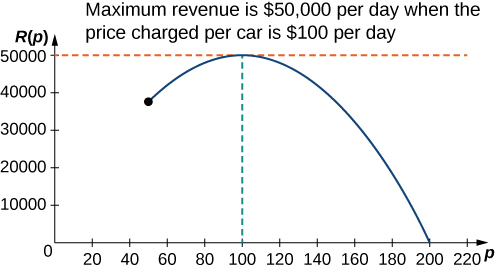
Step 6: Since is a continuous function over the closed, bounded interval it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is Therefore, the critical point is When When When Therefore, the absolute maximum occurs at The car rental company should charge per day per car to maximize revenue as shown in the following figure.
A car rental company charges its customers dollars per day, where It has found that the number of cars rented per day can be modeled by the linear function How much should the company charge each customer to maximize revenue?
The company should charge per car per day.
A rectangle is to be inscribed in the ellipse
What should the dimensions of the rectangle be to maximize its area? What is the maximum area?
Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let be the length of the rectangle and be its width. Let be the area of the rectangle.

Step 2: The problem is to maximize
Step 3: The area of the rectangle is
Step 4: Let be the corner of the rectangle that lies in the first quadrant, as shown in [link] . We can write length and width Since and we have Therefore, the area is
Step 5: From [link] , we see that to inscribe a rectangle in the ellipse, the -coordinate of the corner in the first quadrant must satisfy Therefore, the problem reduces to looking for the maximum value of over the open interval Since will have an absolute maximum (and absolute minimum) over the closed interval we consider over the interval If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.
Step 6: As mentioned earlier, is a continuous function over the closed, bounded interval Therefore, it has an absolute maximum (and absolute minimum). At the endpoints and For Therefore, the maximum must occur at a critical point. Taking the derivative of we obtain
To find critical points, we need to find where We can see that if is a solution of
then must satisfy
Therefore, Thus, are the possible solutions of [link] . Since we are considering over the interval is a possibility for a critical point, but is not. Therefore, we check whether is a solution of [link] . Since is a solution of [link] , we conclude that is the only critical point of in the interval Therefore, must have an absolute maximum at the critical point To determine the dimensions of the rectangle, we need to find the length and the width If then
Therefore, the dimensions of the rectangle are and The area of this rectangle is

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?