| << Chapter < Page | Chapter >> Page > |
Determine the maximum area if we want to make the same rectangular garden as in [link] , but we have ft of fencing.
The maximum area is
Now let’s look at a general strategy for solving optimization problems similar to [link] .
Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.
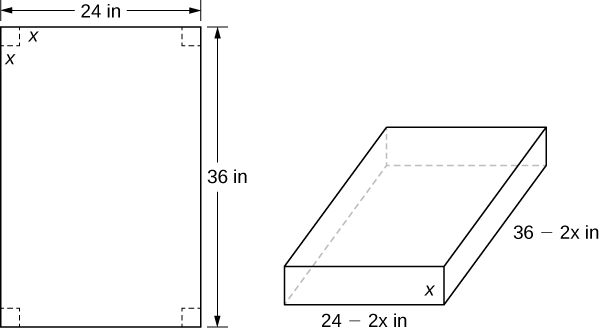
An open-top box is to be made from a in. by in. piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?
Step 1: Let be the side length of the square to be removed from each corner ( [link] ). Then, the remaining four flaps can be folded up to form an open-top box. Let be the volume of the resulting box.
Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize
Step 3: As mentioned in step are trying to maximize the volume of a box. The volume of a box is where are the length, width, and height, respectively.
Step 4: From [link] , we see that the height of the box is inches, the length is inches, and the width is inches. Therefore, the volume of the box is
Step 5: To determine the domain of consideration, let’s examine [link] . Certainly, we need Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for over the open interval Since is a continuous function over the closed interval we know will have an absolute maximum over the closed interval. Therefore, we consider over the closed interval and check whether the absolute maximum occurs at an interior point.
Step 6: Since is a continuous function over the closed, bounded interval must have an absolute maximum (and an absolute minimum). Since at the endpoints and for the maximum must occur at a critical point. The derivative is
To find the critical points, we need to solve the equation
Dividing both sides of this equation by the problem simplifies to solving the equation
Using the quadratic formula, we find that the critical points are
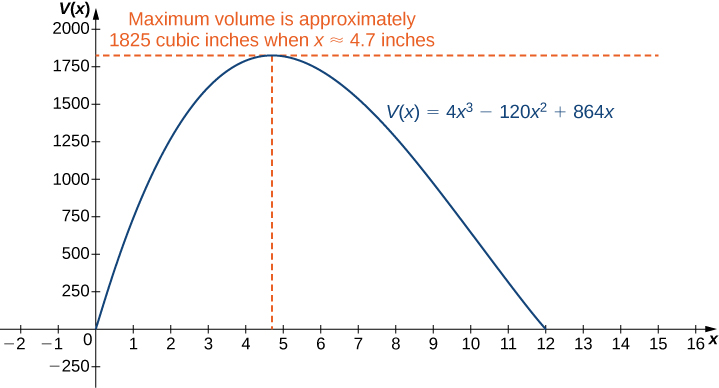
Since is not in the domain of consideration, the only critical point we need to consider is Therefore, the volume is maximized if we let The maximum volume is as shown in the following graph.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?