| << Chapter < Page | Chapter >> Page > |
One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.
The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in [link] , we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.
A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides ( [link] ). Given ft of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?
Let denote the length of the side of the garden perpendicular to the rock wall and denote the length of the side parallel to the rock wall. Then the area of the garden is
We want to find the maximum possible area subject to the constraint that the total fencing is From [link] , the total amount of fencing used will be Therefore, the constraint equation is
Solving this equation for we have Thus, we can write the area as
Before trying to maximize the area function we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need and Since if then Therefore, we are trying to determine the maximum value of for over the open interval We do not know that a function necessarily has a maximum value over an open interval. However, we do know that a continuous function has an absolute maximum (and absolute minimum) over a closed interval. Therefore, let’s consider the function over the closed interval If the maximum value occurs at an interior point, then we have found the value in the open interval that maximizes the area of the garden. Therefore, we consider the following problem:
Maximize over the interval
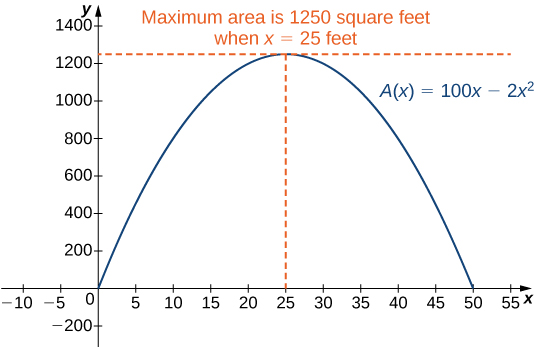
As mentioned earlier, since is a continuous function on a closed, bounded interval, by the extreme value theorem, it has a maximum and a minimum. These extreme values occur either at endpoints or critical points. At the endpoints, Since the area is positive for all in the open interval the maximum must occur at a critical point. Differentiating the function we obtain
Therefore, the only critical point is ( [link] ). We conclude that the maximum area must occur when Then we have To maximize the area of the garden, let ft and The area of this garden is

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?