1. Home
  2. Calculus volume 1
  3. Applications of derivatives
  4. Derivatives and the shape of a

4.5 Derivatives and the shape of a graph  (Page 2/14)

<< Chapter < Page
  Calculus volume 1     Page 2 / 14
Chapter >> Page >

Using [link] , we summarize the main results regarding local extrema.

  • If a continuous function f has a local extremum, it must occur at a critical point c .
  • The function has a local extremum at the critical point c if and only if the derivative f ′ switches sign as x increases through c .
  • Therefore, to test whether a function has a local extremum at a critical point c , we must determine the sign of f ′ ( x ) to the left and right of c .

This result is known as the first derivative test    .

First derivative test

Suppose that f is a continuous function over an interval I containing a critical point c . If f is differentiable over I , except possibly at point c , then f ( c ) satisfies one of the following descriptions:

  1. If f ′ changes sign from positive when x < c to negative when x > c , then f ( c ) is a local maximum of f .
  2. If f ′ changes sign from negative when x < c to positive when x > c , then f ( c ) is a local minimum of f .
  3. If f ′ has the same sign for x < c and x > c , then f ( c ) is neither a local maximum nor a local minimum of f .

We can summarize the first derivative test as a strategy for locating local extrema.

Problem-solving strategy: using the first derivative test

Consider a function f that is continuous over an interval I .

  1. Find all critical points of f and divide the interval I into smaller intervals using the critical points as endpoints.
  2. Analyze the sign of f ′ in each of the subintervals. If f ′ is continuous over a given subinterval (which is typically the case), then the sign of f ′ in that subinterval does not change and, therefore, can be determined by choosing an arbitrary test point x in that subinterval and by evaluating the sign of f ′ at that test point. Use the sign analysis to determine whether f is increasing or decreasing over that interval.
  3. Use [link] and the results of step 2 to determine whether f has a local maximum, a local minimum, or neither at each of the critical points.

Now let’s look at how to use this strategy to locate all local extrema for particular functions.

Using the first derivative test to find local extrema

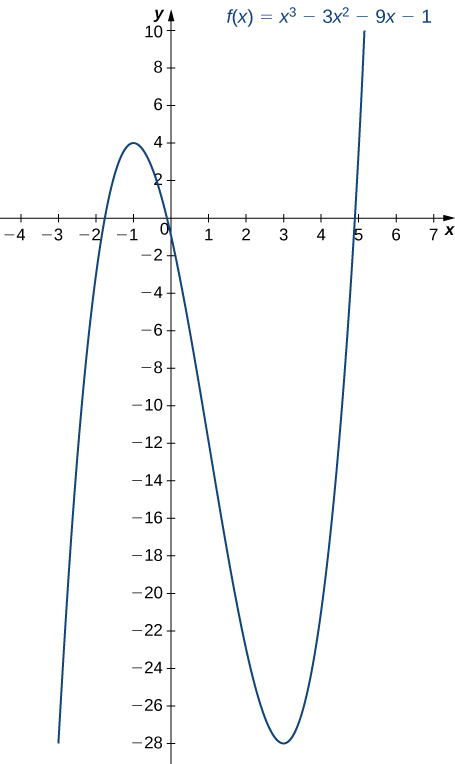
Use the first derivative test to find the location of all local extrema for f ( x ) = x 3 − 3 x 2 − 9 x − 1 . Use a graphing utility to confirm your results.

Step 1. The derivative is f ′ ( x ) = 3 x 2 − 6 x − 9 . To find the critical points, we need to find where f ′ ( x ) = 0 . Factoring the polynomial, we conclude that the critical points must satisfy

3 ( x 2 − 2 x − 3 ) = 3 ( x − 3 ) ( x + 1 ) = 0 .

Therefore, the critical points are x = 3 , −1 . Now divide the interval ( − ∞ , ∞ ) into the smaller intervals ( − ∞ , −1 ) , ( −1 , 3 ) and ( 3 , ∞ ) .

Step 2. Since f ′ is a continuous function, to determine the sign of f ′ ( x ) over each subinterval, it suffices to choose a point over each of the intervals ( − ∞ , −1 ) , ( −1 , 3 ) and ( 3 , ∞ ) and determine the sign of f ′ at each of these points. For example, let’s choose x = −2 , x = 0 , and x = 4 as test points.

Interval Test Point Sign of f ′ ( x ) = 3 ( x − 3 ) ( x + 1 ) at Test Point Conclusion
( − ∞ , −1 ) x = −2 ( + ) ( − ) ( − ) = + f is increasing.
( −1 , 3 ) x = 0 ( + ) ( − ) ( + ) = − f is decreasing.
( 3 , ∞ ) x = 4 ( + ) ( + ) ( + ) = + f is increasing.

Step 3. Since f ′ switches sign from positive to negative as x increases through 1 , f has a local maximum at x = −1 . Since f ′ switches sign from negative to positive as x increases through 3 , f has a local minimum at x = 3 . These analytical results agree with the following graph.

The function f(x) = x3 – 3x2 – 9x – 1 is graphed. It has a maximum at x = −1 and a minimum at x = 3. The function is increasing before x = −1, decreasing until x = 3, and then increasing after that.
The function f has a maximum at x = −1 and a minimum at x = 3
Got questions? Get instant answers now!
Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 1. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11964/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?

Ask