4.3 Maxima and minima  (Page 2/15)

The proof of the extreme value theorem is beyond the scope of this text. Typically, it is proved in a course on real analysis. There are a couple of key points to note about the statement of this theorem. For the extreme value theorem to apply, the function must be continuous over a closed, bounded interval. If the interval $I$ is open or the function has even one point of discontinuity, the function may not have an absolute maximum or absolute minimum over $I.$ For example, consider the functions shown in [link] (d), (e), and (f). All three of these functions are defined over bounded intervals. However, the function in graph (e) is the only one that has both an absolute maximum and an absolute minimum over its domain. The extreme value theorem cannot be applied to the functions in graphs (d) and (f) because neither of these functions is continuous over a closed, bounded interval. Although the function in graph (d) is defined over the closed interval $[0,4],$ the function is discontinuous at $x=2.$ The function has an absolute maximum over $[0,4]$ but does not have an absolute minimum. The function in graph (f) is continuous over the half-open interval $[0,2),$ but is not defined at $x=2,$ and therefore is not continuous over a closed, bounded interval. The function has an absolute minimum over $[0,2),$ but does not have an absolute maximum over $[0,2).$ These two graphs illustrate why a function over a bounded interval may fail to have an absolute maximum and/or absolute minimum.

Before looking at how to find absolute extrema, let’s examine the related concept of local extrema. This idea is useful in determining where absolute extrema occur.

Local extrema and critical points

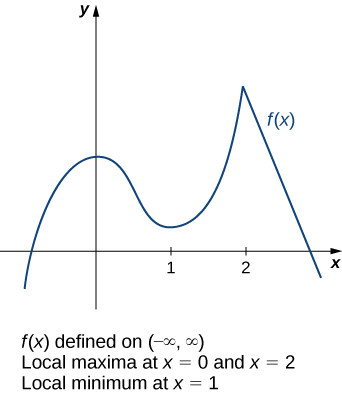
Consider the function $f$ shown in [link] . The graph can be described as two mountains with a valley in the middle. The absolute maximum value of the function occurs at the higher peak, at $x=2.$ However, $x=0$ is also a point of interest. Although $f\left(0\right)$ is not the largest value of $f,$ the value $f\left(0\right)$ is larger than $f\left(x\right)$ for all $x$ near 0. We say $f$ has a local maximum at $x=0.$ Similarly, the function $f$ does not have an absolute minimum, but it does have a local minimum at $x=1$ because $f\left(1\right)$ is less than $f\left(x\right)$ for $x$ near 1.

Note that if $f$ has an absolute extremum at $c$ and $f$ is defined over an interval containing $c,$ then $f(c)$ is also considered a local extremum. If an absolute extremum for a function $f$ occurs at an endpoint, we do not consider that to be a local extremum, but instead refer to that as an endpoint extremum.

Given the graph of a function $f,$ it is sometimes easy to see where a local maximum or local minimum occurs. However, it is not always easy to see, since the interesting features on the graph of a function may not be visible because they occur at a very small scale. Also, we may not have a graph of the function. In these cases, how can we use a formula for a function to determine where these extrema occur?