4.3 Maxima and minima

Given a particular function, we are often interested in determining the largest and smallest values of the function. This information is important in creating accurate graphs. Finding the maximum and minimum values of a function also has practical significance because we can use this method to solve optimization problems, such as maximizing profit, minimizing the amount of material used in manufacturing an aluminum can, or finding the maximum height a rocket can reach. In this section, we look at how to use derivatives to find the largest and smallest values for a function.

Absolute extrema

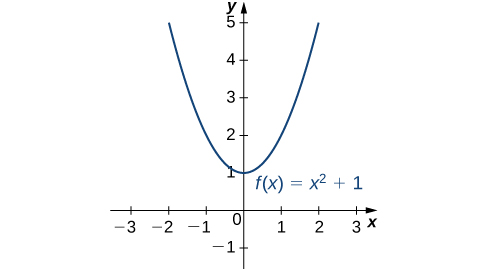
Consider the function $f(x)=x^2+1$ over the interval $(\text{−}\infty ,\infty ).$ As $x\to \text{±}\infty ,$ $f(x)\to \infty .$ Therefore, the function does not have a largest value. However, since $x^2+1\ge 1$ for all real numbers $x$ and $x^2+1=1$ when $x=0,$ the function has a smallest value, 1, when $x=0.$ We say that 1 is the absolute minimum of $f(x)=x^2+1$ and it occurs at $x=0.$ We say that $f(x)=x^2+1$ does not have an absolute maximum (see the following figure).

Before proceeding, let’s note two important issues regarding this definition. First, the term absolute here does not refer to absolute value. An absolute extremum may be positive, negative, or zero. Second, if a function $f$ has an absolute extremum over an interval $I$ at $c,$ the absolute extremum is $f(c).$ The real number $c$ is a point in the domain at which the absolute extremum occurs. For example, consider the function $f(x)=1\text{/}(x^2+1)$ over the interval $(\text{−}\infty ,\infty ).$ Since

for all real numbers $x,$ we say $f$ has an absolute maximum over $(\text{−}\infty ,\infty )$ at $x=0.$ The absolute maximum is $f(0)=1.$ It occurs at $x=0,$ as shown in [link] (b).

A function may have both an absolute maximum and an absolute minimum, just one extremum, or neither. [link] shows several functions and some of the different possibilities regarding absolute extrema. However, the following theorem, called the Extreme Value Theorem , guarantees that a continuous function $f$ over a closed, bounded interval $[a,b]$ has both an absolute maximum and an absolute minimum.