| << Chapter < Page | Chapter >> Page > |
Two airplanes are flying in the air at the same height: airplane A is flying east at 250 mi/h and airplane B is flying north at If they are both heading to the same airport, located 30 miles east of airplane A and 40 miles north of airplane B , at what rate is the distance between the airplanes changing?
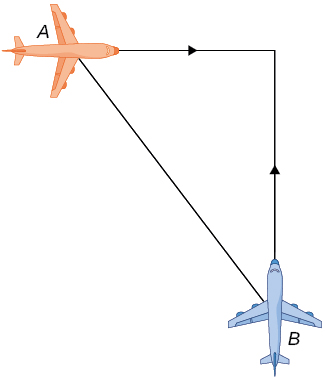
The distance is decreasing at
You and a friend are riding your bikes to a restaurant that you think is east; your friend thinks the restaurant is north. You both leave from the same point, with you riding at 16 mph east and your friend riding north. After you traveled at what rate is the distance between you changing?
Two buses are driving along parallel freeways that are apart, one heading east and the other heading west. Assuming that each bus drives a constant find the rate at which the distance between the buses is changing when they are apart, heading toward each other.
The distance between them shrinks at a rate of
A 6-ft-tall person walks away from a 10-ft lamppost at a constant rate of What is the rate that the tip of the shadow moves away from the pole when the person is away from the pole?
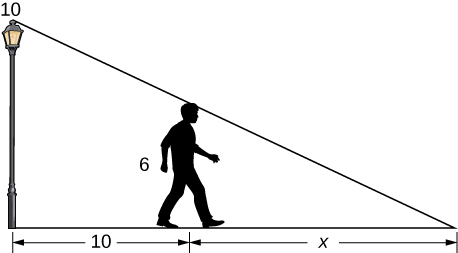
Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is 10 ft from the pole?
ft/sec
A 5-ft-tall person walks toward a wall at a rate of 2 ft/sec. A spotlight is located on the ground 40 ft from the wall. How fast does the height of the person’s shadow on the wall change when the person is 10 ft from the wall?
Using the previous problem, what is the rate at which the shadow changes when the person is 10 ft from the wall, if the person is walking away from the wall at a rate of 2 ft/sec?
It grows at a rate ft/sec
A helicopter starting on the ground is rising directly into the air at a rate of 25 ft/sec. You are running on the ground starting directly under the helicopter at a rate of 10 ft/sec. Find the rate of change of the distance between the helicopter and yourself after 5 sec.
Using the previous problem, what is the rate at which the distance between you and the helicopter is changing when the helicopter has risen to a height of 60 ft in the air, assuming that, initially, it was 30 ft above you?
The distance is increasing at ft/sec
For the following exercises, draw and label diagrams to help solve the related-rates problems.
The side of a cube increases at a rate of m/sec. Find the rate at which the volume of the cube increases when the side of the cube is 4 m.
The volume of a cube decreases at a rate of m/sec. Find the rate at which the side of the cube changes when the side of the cube is 2 m.
m/sec
The radius of a circle increases at a rate of m/sec. Find the rate at which the area of the circle increases when the radius is 5 m.
The radius of a sphere decreases at a rate of m/sec. Find the rate at which the surface area decreases when the radius is 10 m.
m 2 /sec
The radius of a sphere increases at a rate of m/sec. Find the rate at which the volume increases when the radius is m.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?