d
d
(
x
−
n
)
=
0
(
x
n
)
−
1
(
n
x
n
−
1
)
(
x
n
)
2
.
Simplifying, we see that
d
d
(
x
−
n
)
=
−
n
x
n
−
1
x
2
n
=
−
n
x
(
n
−
1
)
−
2
n
=
−
n
x
−
n
−
1
.
Finally, observe that since
k
=
−
n
, by substituting we have
d
d
x
(
x
k
)
=
k
x
k
−
1
.
□
Using the extended power rule and the constant multiple rule
Use the extended power rule and the constant multiple rule to find
f
(
x
)
=
6
x
2
.
It may seem tempting to use the quotient rule to find this derivative, and it would certainly not be incorrect to do so. However, it is far easier to differentiate this function by first rewriting it as
f
(
x
)
=
6
x
−2
.
f
′
(
x
)
=
d
d
x
(
6
x
2
)
=
d
d
x
(
6
x
−2
)
Rewrite
6
x
2
as
6
x
−2
.
=
6
d
d
x
(
x
−2
)
Apply the constant multiple rule.
=
6
(
−2
x
−3
)
Use the extended power rule to differentiate
x
−2
.
=
−12
x
−3
Simplify.
Got questions? Get instant answers now! Got questions? Get instant answers now!
Combining differentiation rules
As we have seen throughout the examples in this section, it seldom happens that we are called on to apply just one differentiation rule to find the derivative of a given function. At this point, by combining the differentiation rules, we may find the derivatives of any polynomial or rational function. Later on we will encounter more complex combinations of differentiation rules. A good rule of thumb to use when applying several rules is to apply the rules in reverse of the order in which we would evaluate the function.
Combining differentiation rules
For
k
(
x
)
=
3
h
(
x
)
+
x
2
g
(
x
)
, find
k
′
(
x
)
.
Finding this derivative requires the sum rule, the constant multiple rule, and the product rule.
k
′
(
x
)
=
d
d
x
(
3
h
(
x
)
+
x
2
g
(
x
)
)
=
d
d
x
(
3
h
(
x
)
)
+
d
d
x
(
x
2
g
(
x
)
)
Apply the sum rule.
=
3
d
d
x
(
h
(
x
)
)
+
(
d
d
x
(
x
2
)
g
(
x
)
+
d
d
x
(
g
(
x
)
)
x
2
)
Apply the constant multiple rule to
differentiate
3
h
(
x
)
and the product
rule to differentiate
x
2
g
(
x
)
.
=
3
h
′
(
x
)
+
2
x
g
(
x
)
+
g
′
(
x
)
x
2
Got questions? Get instant answers now! Got questions? Get instant answers now!
Extending the product rule
For
k
(
x
)
=
f
(
x
)
g
(
x
)
h
(
x
)
, express
k
′
(
x
) in terms of
f
(
x
)
,
g
(
x
)
,
h
(
x
)
, and their derivatives.
We can think of the function
k
(
x
) as the product of the function
f
(
x
)
g
(
x
) and the function
h
(
x
)
. That is,
k
(
x
)
=
(
f
(
x
)
g
(
x
)
)
·
h
(
x
)
. Thus,
k
′
(
x
)
=
d
d
x
(
f
(
x
)
g
(
x
)
)
·
h
(
x
)
+
d
d
x
(
h
(
x
)
)
·
(
f
(
x
)
g
(
x
)
)
Apply the product rule to the product
of
f
(
x
)
g
(
x
)
and
h
(
x
)
.
=
(
f
′
(
x
)
g
(
x
)
+
g
′
(
x
)
f
(
x
)
h
)
(
x
)
+
h
′
(
x
)
f
(
x
)
g
(
x
)
Apply the product rule to
f
(
x
)
g
(
x
)
.
=
f
′
(
x
)
g
(
x
)
h
(
x
)
+
f
(
x
)
g
′
(
x
)
h
(
x
)
+
f
(
x
)
g
(
x
)
h
′
(
x
).
Simplify.
Got questions? Get instant answers now! Got questions? Get instant answers now!
Combining the quotient rule and the product rule
For
h
(
x
)
=
2
x
3
k
(
x
)
3
x
+
2
, find
h
′
(
x
)
.
This procedure is typical for finding the derivative of a rational function.
h
′
(
x
)
=
d
d
x
(
2
x
3
k
(
x
)
)
·
(
3
x
+
2
)
−
d
d
x
(
3
x
+
2
)
·
(
2
x
3
k
(
x
)
)
(
3
x
+
2
)
2
Apply the quotient rule.
=
(
6
x
2
k
(
x
)
+
k
′
(
x
)
·
2
x
3
)
(
3
x
+
2
)
−
3
(
2
x
3
k
(
x
)
)
(
3
x
+
2
)
2
Apply the product rule to find
d
d
x
(
2
x
3
k
(
x
)
)
.
Use
d
d
x
(
3
x
+
2
)
=
3
.
=
−6
x
3
k
(
x
)
+
18
x
3
k
(
x
)
+
12
x
2
k
(
x
)
+
6
x
4
k
′
(
x
)
+
4
x
3
k
′
(
x
)
(
3
x
+
2
)
2
Simplify.
Got questions? Get instant answers now! Got questions? Get instant answers now!
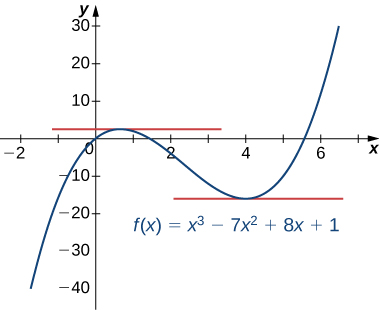
Determining where a function has a horizontal tangent
Determine the values of
x for which
f
(
x
)
=
x
3
−
7
x
2
+
8
x
+
1 has a horizontal tangent line.
To find the values of
x for which
f
(
x
) has a horizontal tangent line, we must solve
f
′
(
x
)
=
0
. Since
f
′
(
x
)
=
3
x
2
−
14
x
+
8
=
(
3
x
−
2
)
(
x
−
4
)
,
we must solve
(
3
x
−
2
)
(
x
−
4
)
=
0
. Thus we see that the function has horizontal tangent lines at
x
=
2
3 and
x
=
4 as shown in the following graph.
This function has horizontal tangent lines at
x = 2/3 and
x = 4. Got questions? Get instant answers now! Got questions? Get instant answers now!