| << Chapter < Page | Chapter >> Page > |
Visit the following applet to experiment with finding values of for selected values of ε :
[link] shows how you can use this definition to prove a statement about the limit of a specific function at a specified value.
Prove that
Let
The first part of the definition begins “For every This means we must prove that whatever follows is true no matter what positive value of ε is chosen. By stating “Let we signal our intent to do so.
Choose
The definition continues with “there exists a ” The phrase “there exists” in a mathematical statement is always a signal for a scavenger hunt. In other words, we must go and find So, where exactly did come from? There are two basic approaches to tracking down One method is purely algebraic and the other is geometric.
We begin by tackling the problem from an algebraic point of view. Since ultimately we want we begin by manipulating this expression: is equivalent to which in turn is equivalent to Last, this is equivalent to Thus, it would seem that is appropriate.
We may also find through geometric methods. [link] demonstrates how this is done.
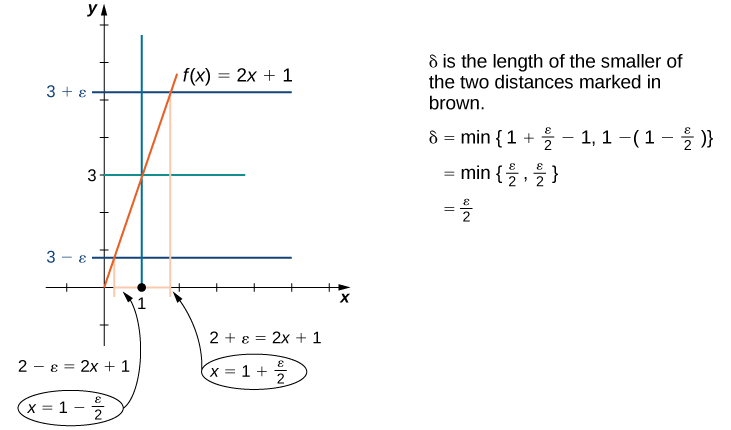
Assume When has been chosen, our goal is to show that if then To prove any statement of the form “If this, then that,” we begin by assuming “this” and trying to get “that.”
Thus,
The following Problem-Solving Strategy summarizes the type of proof we worked out in [link] .
Complete the proof that by filling in the blanks.
Let _____.
Choose
Assume
Thus,
We begin by filling in the blanks where the choices are specified by the definition. Thus, we have
Let
Choose
Assume (or equivalently,
Thus,
Focusing on the final line of the proof, we see that we should choose
We now complete the final write-up of the proof:
Let
Choose
Assume (or equivalently,
Thus,

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?