2.4 Continuity  (Page 7/16)

Discontinuous at $x=1$ with $\underset{x\to \mathrm{-1}}{\text{lim}}f\left(x\right)=\mathrm{-1}$ and $\underset{x\to 2}{\text{lim}}f\left(x\right)=4$

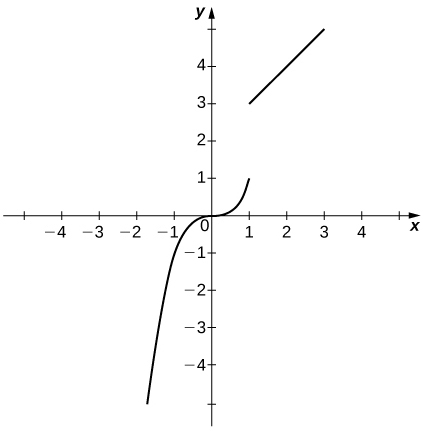
Discontinuous at $x=2$ but continuous elsewhere with $\underset{x\to 0}{\text{lim}}f\left(x\right)=\frac{1}{2}$

$f\left(t\right)=\frac{2}{e^t-e^{-t}}$ is continuous everywhere.

If the left- and right-hand limits of $f\left(x\right)$ as $x\to a$ exist and are equal, then f cannot be discontinuous at $x=a.$

If a function is not continuous at a point, then it is not defined at that point.

According to the IVT, $\text{cos}x-\text{sin}x-x=2$ has a solution over the interval $\left[\mathrm{-1},1\right].$

If $f\left(x\right)$ is continuous such that $f\left(a\right)$ and $f\left(b\right)$ have opposite signs, then $f\left(x\right)=0$ has exactly one solution in $\left[a,b\right].$

The function $f\left(x\right)=\frac{x^2-4x+3}{x^2-1}$ is continuous over the interval $\left[0,3\right].$

If $f\left(x\right)$ is continuous everywhere and $f\left(a\right),f\left(b\right)>0,$ then there is no root of $f\left(x\right)$ in the interval $\left[a,b\right].$

To simplify the calculation of a model with many interacting particles, after some threshold value $r=R,$ we approximate F as zero.

1. Explain the physical reasoning behind this assumption.
2. What is the force equation?
3. Evaluate the force F using both Coulomb’s law and our approximation, assuming two protons with a charge magnitude of $1.6022\times {10}^{\mathrm{-19}}\text{coulombs (C)},$ and the Coulomb constant $k_e=8.988\times {10}^9{\text{Nm}}^2\text{/}{\text{C}}^2$ are 1 m apart. Also, assume $R<1\text{m}.$ How much inaccuracy does our approximation generate? Is our approximation reasonable?
4. Is there any finite value of R for which this system remains continuous at R ?

Instead of making the force 0 at R , instead we let the force be 10 ⁻²⁰ for $r\ge R.$ Assume two protons, which have a magnitude of charge $1.6022\times {10}^{\mathrm{-19}}\text{C},$ and the Coulomb constant $k_e=8.988\times {10}^9{\text{Nm}}^2\text{/}{\text{C}}^2.$ Is there a value R that can make this system continuous? If so, find it.

[T] Determine the value and units of k given that the mass of the rocket on Earth is 3 million kg. ( Hint : The distance from the center of Earth to its surface is 6378 km.)

[T] After a certain distance D has passed, the gravitational effect of Earth becomes quite negligible, so we can approximate the force function by $F\left(d\right)=\{\begin{array}{ll}-\frac{mk}{d^2}\hfill & \text{if}d<D\hfill \\ \mathrm{10,000}\hfill & \text{if}d\ge D\hfill \end{array}.$ Find the necessary condition D such that the force function remains continuous.

As the rocket travels away from Earth’s surface, there is a distance D where the rocket sheds some of its mass, since it no longer needs the excess fuel storage. We can write this function as $F\left(d\right)=\{\begin{array}{l}-\frac{m_{1}k}{d^2}\text{if}d<D\hfill \\ -\frac{m_{2}k}{d^2}\text{if}d\ge D\hfill \end{array}.$ Is there a D value such that this function is continuous, assuming $m_1\ne m_2?$

$f\left(\theta \right)=\text{sin}\theta$

$g\left(x\right)=\left|x\right|$

Where is $f\left(x\right)=\{\begin{array}{l}0\text{if}x\text{is irrational}\\ 1\text{if}x\text{is rational}\end{array}$ continuous?