| << Chapter < Page | Chapter >> Page > |
Because and by using the squeeze theorem we conclude that
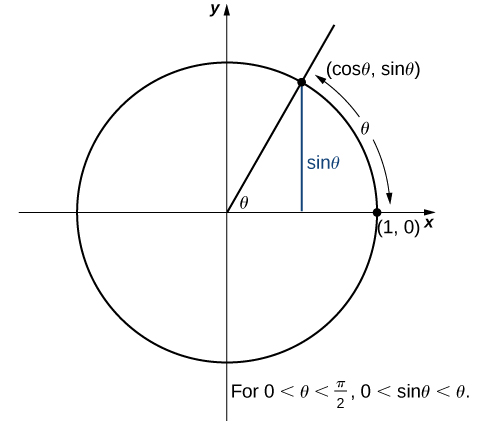
To see that as well, observe that for and hence, Consequently, It follows that An application of the squeeze theorem produces the desired limit. Thus, since and
Next, using the identity for we see that
We now take a look at a limit that plays an important role in later chapters—namely, To evaluate this limit, we use the unit circle in [link] . Notice that this figure adds one additional triangle to [link] . We see that the length of the side opposite angle θ in this new triangle is Thus, we see that for
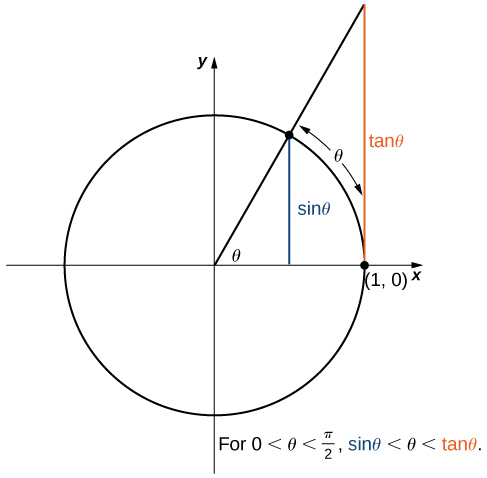
By dividing by in all parts of the inequality, we obtain
Equivalently, we have
Since we conclude that By applying a manipulation similar to that used in demonstrating that we can show that Thus,
In [link] we use this limit to establish This limit also proves useful in later chapters.
Evaluate
In the first step, we multiply by the conjugate so that we can use a trigonometric identity to convert the cosine in the numerator to a sine:
Therefore,
Some of the geometric formulas we take for granted today were first derived by methods that anticipate some of the methods of calculus. The Greek mathematician Archimedes (ca. 287−212; BCE) was particularly inventive, using polygons inscribed within circles to approximate the area of the circle as the number of sides of the polygon increased. He never came up with the idea of a limit, but we can use this idea to see what his geometric constructions could have predicted about the limit.
We can estimate the area of a circle by computing the area of an inscribed regular polygon. Think of the regular polygon as being made up of n triangles. By taking the limit as the vertex angle of these triangles goes to zero, you can obtain the area of the circle. To see this, carry out the following steps:
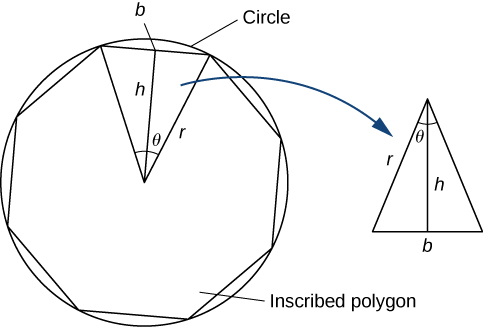
The technique of estimating areas of regions by using polygons is revisited in Introduction to Integration .

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?