| << Chapter < Page | Chapter >> Page > |
Compare the relative severity of a magnitude earthquake with a magnitude earthquake.
The magnitude earthquake is roughly times as severe as the magnitude earthquake.
The hyperbolic functions are defined in terms of certain combinations of and These functions arise naturally in various engineering and physics applications, including the study of water waves and vibrations of elastic membranes. Another common use for a hyperbolic function is the representation of a hanging chain or cable, also known as a catenary ( [link] ). If we introduce a coordinate system so that the low point of the chain lies along the -axis, we can describe the height of the chain in terms of a hyperbolic function. First, we define the hyperbolic functions .

Hyperbolic cosine
Hyperbolic sine
Hyperbolic tangent
Hyperbolic cosecant
Hyperbolic secant
Hyperbolic cotangent
The name cosh rhymes with “gosh,” whereas the name sinh is pronounced “cinch.” Tanh , sech , csch , and coth are pronounced “tanch,” “seech,” “coseech,” and “cotanch,” respectively.
Using the definition of and principles of physics, it can be shown that the height of a hanging chain, such as the one in [link] , can be described by the function for certain constants and
But why are these functions called hyperbolic functions ? To answer this question, consider the quantity Using the definition of and we see that
This identity is the analog of the trigonometric identity Here, given a value the point lies on the unit hyperbola ( [link] ).
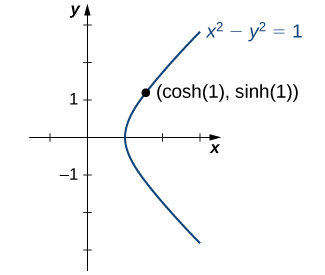
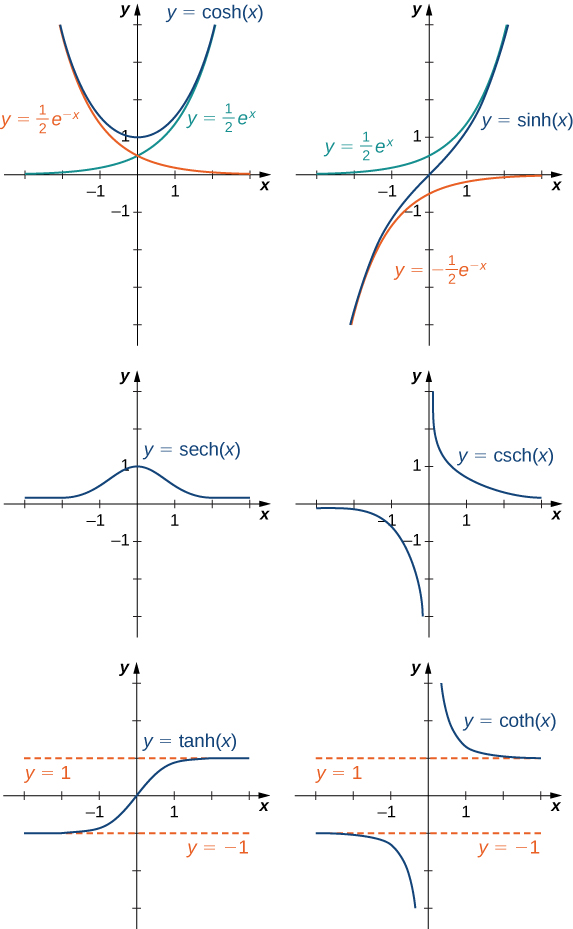
To graph and we make use of the fact that both functions approach as since as As approaches whereas approaches Therefore, using the graphs of and as guides, we graph and To graph we use the fact that for all as and as The graphs of the other three hyperbolic functions can be sketched using the graphs of and ( [link] ).
The identity shown in [link] , is one of several identities involving the hyperbolic functions, some of which are listed next. The first four properties follow easily from the definitions of hyperbolic sine and hyperbolic cosine. Except for some differences in signs, most of these properties are analogous to identities for trigonometric functions.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?