| << Chapter < Page | Chapter >> Page > |
What happens as To answer this question, we let and write
and examine the behavior of as using a table of values ( [link] ).
Looking at this table, it appears that is approaching a number between and as In fact, does approach some number as We call this number . To six decimal places of accuracy,
The letter was first used to represent this number by the Swiss mathematician Leonhard Euler during the 1720s. Although Euler did not discover the number, he showed many important connections between and logarithmic functions. We still use the notation today to honor Euler’s work because it appears in many areas of mathematics and because we can use it in many practical applications.
Returning to our savings account example, we can conclude that if a person puts dollars in an account at an annual interest rate compounded continuously, then This function may be familiar. Since functions involving base arise often in applications, we call the function the natural exponential function . Not only is this function interesting because of the definition of the number but also, as discussed next, its graph has an important property.
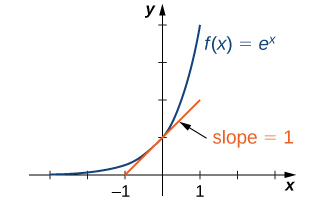
Since we know is increasing on In [link] , we show a graph of along with a tangent line to the graph of at We give a precise definition of tangent line in the next chapter; but, informally, we say a tangent line to a graph of at is a line that passes through the point and has the same “slope” as at that point The function is the only exponential function with tangent line at that has a slope of 1. As we see later in the text, having this property makes the natural exponential function the most simple exponential function to use in many instances.
Suppose is invested in an account at an annual interest rate of compounded continuously.
If is invested in an account at an annual interest rate of compounded continuously, find a formula for the amount of money in the account after years. Find the amount of money after years.
After years, there will be approximately
Using our understanding of exponential functions, we can discuss their inverses, which are the logarithmic functions. These come in handy when we need to consider any phenomenon that varies over a wide range of values, such as pH in chemistry or decibels in sound levels.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?