| << Chapter < Page | Chapter >> Page > |
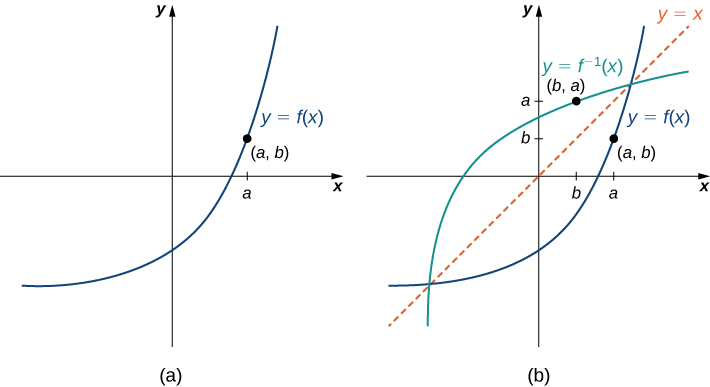
For the graph of in the following image, sketch a graph of by sketching the line and using symmetry. Identify the domain and range of
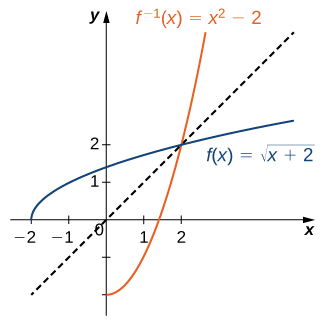
Reflect the graph about the line The domain of is The range of is By using the preceding strategy for finding inverse functions, we can verify that the inverse function is as shown in the graph.
Sketch the graph of and the graph of its inverse using the symmetry property of inverse functions.

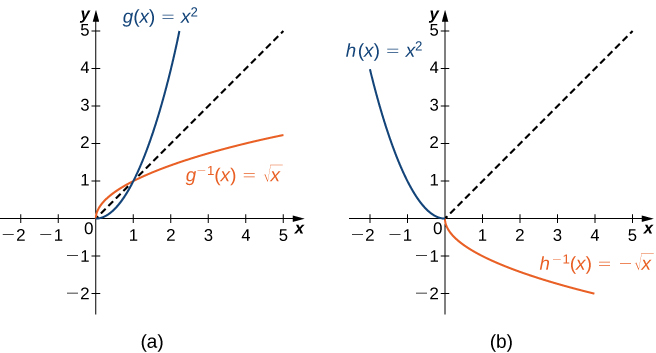
As we have seen, does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of such that the function is one-to-one. This subset is called a restricted domain . By restricting the domain of we can define a new function such that the domain of is the restricted domain of and for all in the domain of Then we can define an inverse function for on that domain. For example, since is one-to-one on the interval we can define a new function such that the domain of is and for all in its domain. Since is a one-to-one function, it has an inverse function, given by the formula On the other hand, the function is also one-to-one on the domain Therefore, we could also define a new function such that the domain of is and for all in the domain of Then is a one-to-one function and must also have an inverse. Its inverse is given by the formula ( [link] ).
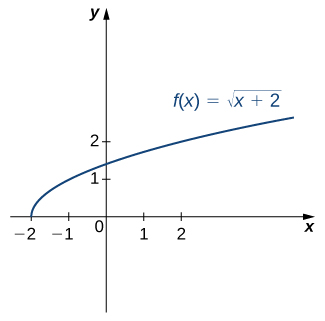
Consider the function

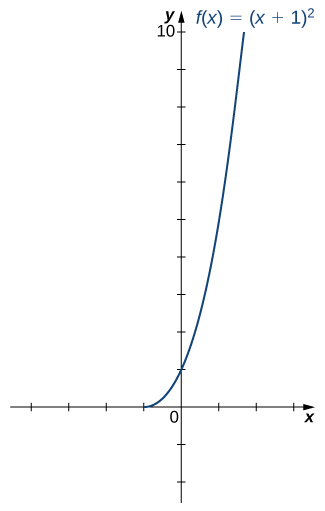
Consider restricted to the domain Verify that is one-to-one on this domain. Determine the domain and range of the inverse of and find a formula for
The domain of is The range of is The inverse function is given by the formula
The six basic trigonometric functions are periodic, and therefore they are not one-to-one. However, if we restrict the domain of a trigonometric function to an interval where it is one-to-one, we can define its inverse. Consider the sine function ( [link] ). The sine function is one-to-one on an infinite number of intervals, but the standard convention is to restrict the domain to the interval By doing so, we define the inverse sine function on the domain such that for any in the interval the inverse sine function tells us which angle in the interval satisfies Similarly, we can restrict the domains of the other trigonometric functions to define inverse trigonometric functions , which are functions that tell us which angle in a certain interval has a specified trigonometric value.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?