| << Chapter < Page | Chapter >> Page > |
Be careful of the signs when you subtract a binomial!
When the denominators of two rational expressions are opposites, it is easy to get a common denominator. We just have to multiply one of the fractions by .
Let’s see how this works.
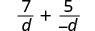 | |
| Multiply the second fraction by . |
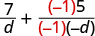 |
| The denominators are the same. |
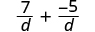 |
| Simplify. |
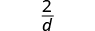 |
Add:
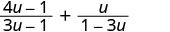 | |
| The denominators are opposites, so multiply the second fraction by . |
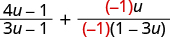 |
| Simplify the second fraction. |
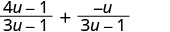 |
| The denominators are the same. Add the numerators. |
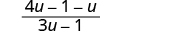 |
| Simplify. |
 |
| Simplify. |
 |
Subtract:
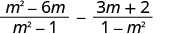 | |
| The denominators are opposites, so multiply the second fraction by . |
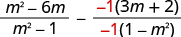 |
| Simplify the second fraction. |
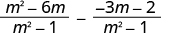 |
| The denominators are the same. Subtract the numerators. |
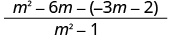 |
| Distribute. | |
| Combine like terms. |
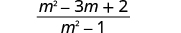 |
| Factor the numerator and denominator. |
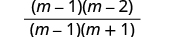 |
| Simplify by removing common factors. |
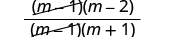 |
| Simplify. |
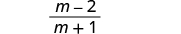 |
Add Rational Expressions with a Common Denominator
In the following exercises, add.
Subtract Rational Expressions with a Common Denominator
In the following exercises, subtract.
Add and Subtract Rational Expressions whose Denominators are Opposites
In the following exercises, add.
In the following exercises, subtract.
Sarah ran 8 miles and then biked 24 miles. Her biking speed is 4 mph faster than her running speed. If represents Sarah’s speed when she ran, then her running time is modeled by the expression and her biking time is modeled by the expression Add the rational expressions to get an expression for the total amount of time Sarah ran and biked.
If Pete can paint a wall in hours, then in one hour he can paint of the wall. It would take Penelope 3 hours longer than Pete to paint the wall, so in one hour she can paint of the wall. Add the rational expressions to get an expression for the part of the wall Pete and Penelope would paint in one hour if they worked together.
Donald thinks that is Is Donald correct? Explain.
Explain how you find the Least Common Denominator of and
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?