| << Chapter < Page | Chapter >> Page > |
Why is there no real number equal to
What is the difference between and
Answers will vary. 9 2 reads: “nine squared” and means nine times itself. The expression reads: “the square root of nine” which gives us the number such that if it were multiplied by itself would give you the number inside of the square root.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
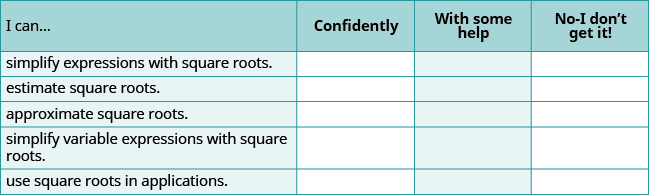
ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?
Name Decimals
In the following exercises, name each decimal.
Write Decimals
In the following exercises, write as a decimal.
three tenths
twenty-seven hundredths
negative twenty and three tenths
Convert Decimals to Fractions or Mixed Numbers
In the following exercises, convert each decimal to a fraction. Simplify the answer if possible.
Locate Decimals on the Number Line
Locate the following decimals on a number line.
ⓐ
ⓑ
ⓒ
ⓓ
Order Decimals
In the following exercises, order each of the following pairs of numbers, using or
Round Decimals
In the following exercises, round each number to the nearest:
ⓐ hundredth
ⓑ tenth
ⓒ whole number.
Add and Subtract Decimals
In the following exercises, add or subtract.
Multiply Decimals
In the following exercises, multiply.
Divide Decimals
In the following exercises, divide.
Use Decimals in Money Applications
In the following exercises, use the strategy for applications to solve.
Miranda got from her ATM. She spent on lunch and on a book. How much money did she have left? Round to the nearest cent if necessary.
Jessie put gallons of gas in her car. One gallon of gas costs How much did Jessie owe for all the gas?
$28.22
A pack of water bottles cost How much did each bottle cost?
Alice bought a roll of paper towels that cost She had a coupon for off, and the store doubled the coupon. How much did Alice pay for the paper towels?
$1.79
Convert Fractions to Decimals
In the following exercises, convert each fraction to a decimal.
Order Decimals and Fractions
In the following exercises, order each pair of numbers, using or
In the following exercises, write each set of numbers in order from least to greatest.
Simplify Expressions Using the Order of Operations

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?